CBSE Class 12 Maths MCQs and Sample Paper for Term-1

Maths Class 12 Sample Paper & MCQs

Maths MCQs for the Class 12 Term 1: CBSE has introduced the scheme of conducting 12th Board Exams twice in a year i.e. the syllabus is divided into Term-1 & Term-2. The students have to appear in the Term-1 Exam for Class 12 on 06th December 2021 where they will be provided with 50 Multiple Choice Questions in 3 sections and they have to attempt 40 questions from the Maths MCQs Class 12 Term 1 Paper. There will be no negative marking for any unanswered question or wrong answer, but do keep in mind if you attempt all questions still only the first 16 MCQ of Section A & B and the first 8 MCQ of Section C will be considered for evaluating final marks. 

CBSE Maths Class 12 MCQs for Term 1

The below provided important Maths MCQs Class 12 Term 1 are from the units that have been discussed in the syllabus which include- Relations and Functions, Algebra, Calculus, and Linear Programming. To help the students have a clear cut idea of how to attempt the exam, we have prepared a sample Maths MCQ Class 12 kind of paper in this article which includes a total of 50 MCQ of Maths Term-1 Class 12. Let's begin with the important Maths MCQ Class 12 Term-1. 

Class 12 Maths Answer key Term-1- Click to Check

Q1. The function f : R → R defined by f(x) = 3 – 4x is

(a) Onto

(b) Not onto

(c) None one-one

(d) None of these

Solution: (a) 

Q2. Let * be a binary operation on Q, defined by a * b = 3𝑎𝑏/5 is

(a) Commutative

(b) Associative

(c) Both (a) and (b)

(d) None of these

Solution: (c) 

Q3. The number of commutative binary operations that can be defined on a set of 2 elements is

(a) 8

(b) 6

(c) 4

(d) 2

Solution: (d)

Q4. Let S = {1, 2, 3, 4, 5} and let A = S × S. Define the relation R on A as follows:

(a, b) R (c, d) iff ad = cb. Then, R is

(a) reflexive only

(b) Symmetric only

(c) Transitive only

(d) Equivalence relation

Solution: (d)

Q5. Let A = {x : -1 ≤ x ≤ 1} and f : A → A is a function defined by f(x) = x |x| then f is

(a) a bijection

(b) injection but not surjection

(c) surjection but not injection

(d) neither injection nor surjection

Solution: (a) 

Q6. Let * be the binary operation on N given by a * b = HCF (a, b) where, a, b ∈ N. Find the value of 22 * 4.

(a) 1

(b) 2

(c) 3

(d) 4

Solution: (b)

Q7. Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is

(a) reflexive but not symmetric

(b) reflexive but not transitive

(c) symmetric and transitive

(d) neither symmetric, nor transitive

Solution: (a) 

Q8. If AB × AC = 2𝑖̂ −4𝑗̂ + 4𝑘̂ , then the are of ΔABC is

(a) 3 sq. units

(b) 4 sq. units

(c) 16 sq. units

(d) 9 sq. units

Solution: (a)

Q9. 

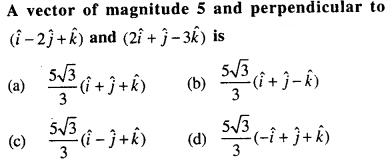
Solution: (a)

Q10. Find the value of λ so that the vectors 2𝑖−4𝑗̂ +𝑘̂  and 4𝑖−8𝑗̂ +𝜆𝑘̂  are parallel.

(a) -1

(b) 3

(c) -4

(d) 2

Solution: (d)

Q11. Let a, b and c be vectors with magnitudes 3, 4 and 5 respectively and a + b + c = 0, then the values of a.b + b.c + c.a is

(a) 47

(b) 25

(c) 50

(d) -25

Solution: (d) 

Q12. If |a| = |b| = 1 and |a + b| = √3, then the value of (3a – 4b).(2a + 5b) is

(a) -21

(b) −21/2

(c) 21

(d) 21/2

Solution: (b)

Q13. In a linear programming problem, the constraints on the decision variables x and y are 𝑥 − 3𝑦 ≥ 0, 𝑦 ≥ 0, 0 ≤ 𝑥 ≤ 3. The feasible region

a) is not in the first quadrant

b) is bounded in the first quadrant

c) is unbounded in the first quadrant

d) does not exist

Solution: (b)

Q14. The length of the longer diagonal of the parallelogram is constructed on 5a + 2b and a – 3b. If it is given that |a| = 2√2, |b| = 3 and angle between a and b is 𝜋4, is

(a) 15

(b) √113

(c) √593

(d) √369

Solution: (c)

Q15. The maximum value of f = 4x + 3y subject to constraints x ≥ 0, y ≥ 0, 2x + 3y ≤ 18; x + y ≥ 10 is

(a) 35

(b) 36

(c) 34

(d) none of these

Solution: (d) 

Q16. Objective function of a L.P.P.is

(a) a constant

(b) a function to be optimised

(c) a relation between the variables

(d) none of these

Solution: (b)

Q17. Region represented by x ≥ 0, y ≥ 0 is

(a) first quadrant

(b) second quadrant

(c) third quadrant

(d) fourth quadrant

Solution: (a)

Q18. Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.

(a) 80 at (3, 2)

(b) 75 at (0, 3)

(c) 30 at (3, 0)

(d) 95 at (2, 3)

Solution: (d) 

Q19. Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at

(a) (3, 0)

(b) (1/2,5/2)

(c) (7, 0)

(d) (0, 5)

Solution: (d)

Q20. 

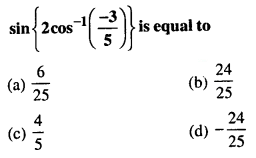
Solution: (d)

Q21.

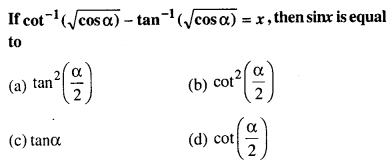
Answer: (a)

Q22. The value of c in mean value theorem for the function f(x) = (x – 3)(x – 6)(x – 9) in [3, 5] is

(a) 6 ± √(13/3)

(b) 6 + √(13/3)

(c) 6 – √(13/3)

(d) None of these

Answer: (c) 

Q23.

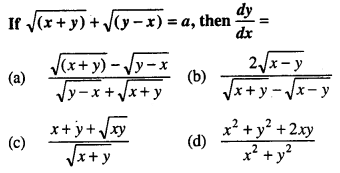
Answer: (a)

Q24. The slope of the tangent to the curve x = a sin t, y = a{cot t + log(tan 𝑡/2)} at the point ‘t’ is

(a) tan t

(b) cot t

(c) tan 𝑡/2

(d) None of these

Answer: (a)

Q25. If there is an error of a% in measuring the edge of a cube, then percentage error in its surface area is

(a) 2a%

(b) 𝑎/2 %

(c) 3a%

(d) None of these

Answer: (b) 

Q26. 

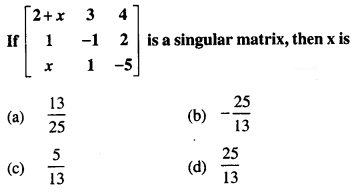
Answer: (b)

Q27. The function f(x) = log (1 + x) – 2𝑥/2+𝑥 is increasing on

(a) (-1, ∞)

(b) (-∞, 0)

(c) (-∞, ∞)

(d) None of these

Answer: (a) 

Q28. The function f(x) = x + 4/𝑥 has

(a) a local maxima at x = 2 and local minima at x = -2

(b) local minima at x = 2, and local maxima at x = -2

(c) absolute maxima at x = 2 and absolute minima at x = -2

(d) absolute minima at x = 2 and absolute maxima at x = -2

Answer: (b)

Q29. If a matrix A is both symmetric and skew-symmetric, then

(a) A is a diagonal matrix

(b) A is a zero matrix

(c) A is a scalar matrix

(d) A is a square matrix

Answer: (b) 

Q30. The number of binary operations that can be defined on a set of 2 elements is

(a) 8

(b) 4

(c) 16

(d) 64

Answer: (c) 

Q31. 

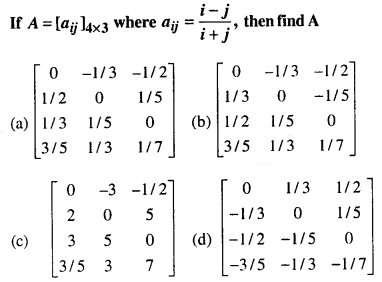
Answer: (b)

Q32. Let T be the set of all triangles in the Euclidean plane, and let a relation R on T be defined as aRb if a is congruent to b ∀ a, b ∈ T. Then R is

(a) reflexive but not transitive

(b) transitive but not symmetric

(c) equivalence

(d) None of these

Answer: (c) 

Q33. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let 𝑓 = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, 𝑓 is best defined as:

a) Surjective function 

b) Injective function

c) Bijective function 

d) function

Answer: (b) 

Q34. 

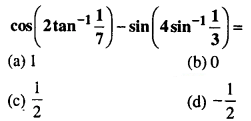
Answer: (b)

Q35. Let us define a relation R in R as aRb if a ≥ b. Then R is

(a) an equivalence relation

(b) reflexive, transitive but not symmetric

(c) symmetric, transitive but not reflexive

(d) neither transitive nor reflexive but symmetric

Answer: (b)

Q36. Let R be a relation on the set N of natural numbers denoted by nRm ⇔ n is a factor of m (i.e. n | m). Then, R is

(a) Reflexive and symmetric

(b) Transitive and symmetric

(c) Equivalence

(d) Reflexive, transitive but not symmetric

Answer: (d) 

Q37. If * is a binary operation on set of integers I defined by a * b = 3a + 4b – 2, then find the value of 4 * 5.

(a) 35

(b) 30

(c) 25

(d) 29

Answer: (b) 

Q38. Given that matrices A and B are of order 3×n and m×5 respectively, then the order of matrix C = 5A +3B is:

a) 3×5 

b) 5×3

c) 3×3 

d) 5×5

Answer: (b)

Q39. The function f : A → B defined by f(x) = 4x + 7, x ∈ R is

(a) one-one

(b) Many-one

(c) Odd

(d) Even

Answer: (a)

Q40. Find the height of the cylinder of maximum volume that can be is cribed in a sphere of radius a.

(a) 2𝑎/3

(b) 2𝑎/√3

(c) 𝑎/3

(d) 2𝑎/3

Answer: (b) 

Q41. The area of a right-angled triangle of the given hypotenuse is maximum when the triangle is

(a) scalene

(b) equilateral

(c) isosceles

(d) None of these

Answer: (c) 

Q42. The equation of the normal to the curves y = sin x at (0, 0) is

(a) x = 0

(b) x + y = 0

(c) y = 0

(d) x – y = 0

Answer: (b)

Q43. The radius of a cylinder is increasing at the rate of 3 m/s and its height is decreasing at the rate of 4 m/s. The rate of change of volume when the radius is 4 m and height is 6 m, is

(a) 80π cu m/s

(b) 144π cu m/s

(c) 80 cu m/s

(d) 64 cu m/s

Answer: (a) 

Q44. Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}, then

a) (2,4) ∈ R 

b) (3,8) ∈ R 

c) (6,8) ∈ R 

d) (8,7) ∈ R

Answer: (c)

Q45. The value of 𝑏 for which the function 𝑓(𝑥) = 𝑥 + 𝑐𝑜𝑠𝑥 + 𝑏 is strictly decreasing over R is:

a) 𝑏 < 1 

b) No value of b exists

c) 𝑏 ≤ 1 

d) 𝑏 ≥ 1

Answer: (b)

Case Study

Deepa rides her car at 25 km/hr. She has to spend Rs.2 per km on diesel and if she rides it at a faster speed of 40km/hr, the diesel cost increases to Rs. 5 per km. She has Rs. 100 to spend on diesel. Let her travel x km with a speed of 25 km/hr and y km with a speed of 40 km/hr. The feasible region or the LPP is shown below-

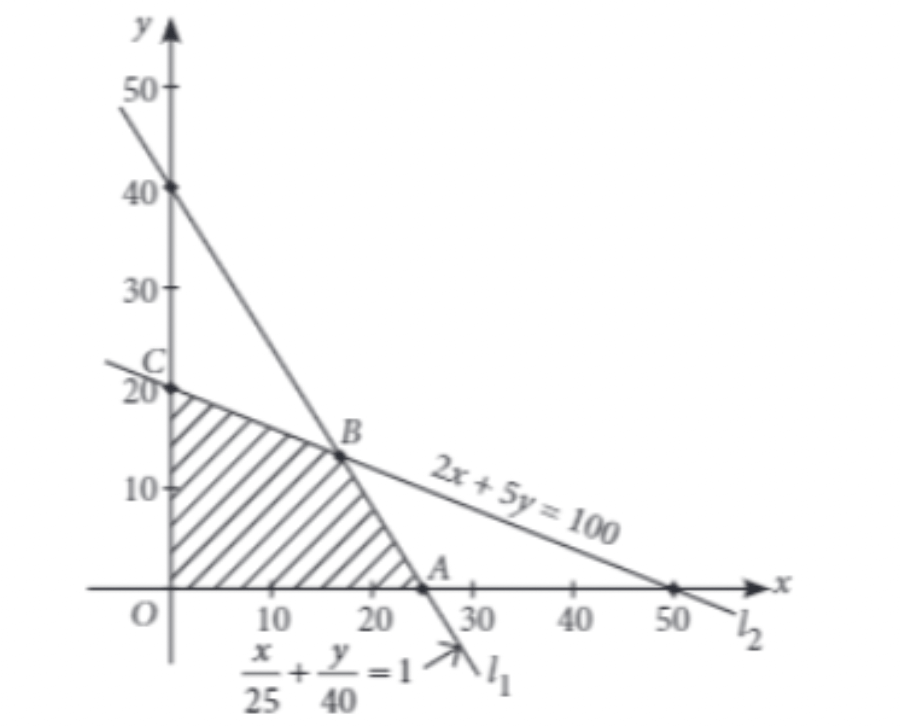
Based on the above information answer the following questions- 

Q46. What is the point of intersection of line l1 & l2. 

a) (40/3, 50/3)

b) (50/3, 40/3)

c) (-50/3, 40/3)

d) (-50/3, -40/3)

Answer: (b)

Q47. The corner points of the feasible region shown in the above graph are- 

a) (0,25), (20,0), (40/3,50/3)

b) (0,0), (25,0), (0,20)

c) (0,0), (40/3,50/3), (0,20)

d) (0,0), (25,0), (50/3, 40/3), (0,20)

Answer: (d)

Q48. If Z = x+y be the objective function and max Z = 30. The maximum value occurs at point- 

a) (50/3, 40/3)

b) (0,0)

c) (25,0)

d) (0,20)

Answer: (a)

Q49. If Z = 6x- 9y be the objective function, then the maximum value of Z is 

a) -20

b) 150 

c) 180

d) 20

Answer: (b) 

Q50. If Z = 6x+ 3y be the objective function, then the maximum value of Z is 

a) 120

b) 130 

c) 0

d) 150

Answer: (c)

CBSE Class 12 Maths Syllabus (Term 1+Term 2)- Click Here

Maths Class 12 Sample Paper 2021

The direct link to practice with the official Class 12 Maths Sample Paper 2021 released by CBSE is attached below. The link for the solution to the sample paper is also provided next to the Maths MCQ Class 12 Term-1. 

Click to Download Class 12 Maths Sample Paper 2021 PDF

Click to Download Class 12 Maths Sample Paper 2021 Solution PDF

CBSE Class 12 Maths Syllabus (Term 1+Term 2)- Click Here

CBSE Class 12 Physics Syllabus (Term 1+Term 2)- Click Here

CBSE Class 12 Chemistry Syllabus (Term 1+Term 2)- Click Here

CBSE Class 12 English Syllabus (Term 1+Term 2)- Click Here