Maths Class 10 Term 2 Answer Key 2022
CBSE Class 10th Maths Answer Key for Term 2 Exam 2022: CBSE has conducted Class 10th Maths Term-1 Exam today on 05th May 2022 and after appearing in the exam, the students must be anxious to check the Answer Key of Maths Term 2 to crosscheck the answers they have attempted. In this article, we have been discussing the correct answers as solved by our esteemed faculty. The students should scroll down the page to check the detailed Maths Class 10 Term 2 Answer Key and connect with us to get correct responses for the questions asked in the Class 10 Maths Term 2 Exam. We will be providing authentic and explained answers to each question asked in the Basic & Standard Mathematics Examination.
Class 10 Maths Term 2 Answer Key 2022
Class 10 Mathematics Term 2 Exam was on 05th May 2022 and lakhs of students across the country are going to appear in this exam. The CBSE 10th term 2 Maths Exam has been commenced from 10:30 am to 12:30 pm. The exam duration would be 2 hours and extra 15 minutes is given for reading the question paper. The exam will be conducted in pen and paper mode. There will be 14 questions in the CBSE Class 10 Term 2 Maths Exam from Algebra, Geometry, Trigonometry, Mensuration, Statistics & Probability chapter as per CBSE Class 10 Maths Syllabus.
CBSE Class 10 Answer Key Maths
Term 2 Maths Answer Key for both Basic & Standard Mathematics Examination has been discussed in this article after the conduction of Maths Term 2 Exam on 05th May 2022.
| CBSE Class 10th Answer Key Mathematics | |
| Exam Conducting Body | Central Board of Secondary Education |
| Exam Name | CBSE Class 10 Maths (Basic & Standard) |
| Category | Answer Key |
| Exam Date | 05th May 2022 |
| Unofficial Answer Key | 05th May 2022 |
| Official Website | https://www.cbse.nic.in/ |
Class 10 Maths Term 2 Question Paper & Solution
Here we will be discussing the complete CBSE Class 10 Term 2 Maths Paper, stay tuned with us and keep refreshing the page.
Class 10 Term 2 Standard Maths Solution [Series- PPQQA/1 Set 1, Paper Code- 30/1/1]
SECTION A
Question 1- Find the sum of first 30 terms of AP: -30, 24, -18,/..
Solution- a= -30, d= 6
= 15 [-60 + 29 (6)]
= 15 [-60+174]
= 15 [114]
= 1710
OR
Question 1- If an AP is Sn = n(4n+1), then find the AP
Solution- S1 = T1 = 5
S2= T1 + T2= 18
S2-S1 = T2= 13
AP= 5, 13, 21, 29, …
Question 2- A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Solution- r1 = 10.5 cm (sphere) and r2 (cone)= 3.5 cm, h2= 3cm
4/3πr³ = n x 1/3πr2² h
4r³ = nr2² h
4 x (105/10)³= n x 35/10 x 35/10 x 3
21 x 6= n
Number of cones formed= 126
Question 3 (a) Find the value of m for which the quadratic equation
(m-1) x² + 2(m-1)x + 1 = 0
Solution- D= 0
4 (m-1)² - 4(m-1) = 0
4 (m-1) [m-1-1]= 0
(m-1) (m-2)= 0
m= 2
(b) Solve the following quadratic equation for x: √3x² + 10x + 7√3= 0
Solution- √3x² + 3x + 7x + 7√3= 0
√3x (x+ √3) + 7 (x + √3)= 0
(x+ √3) [√3x + 7]= 0
x= √3 || x= -7/√3
Question 4- Find the mode of the following frequency distribution:
| Class | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 15 | 10 | 12 | 17 | 4 |
Solution- l= 40, f1= 17, f2= 4, fo= 12
Mode= l + f1-fo / 2f1 - fo- f2
= 40 + 17-12 / 34-12-4 x 10
= 40 + 5/18 x 10
= 40 + 25/9
= 40 + 2.78
= 42.78
Question 5- The product of Rehan's age (in years) 5 years ago and his age 7 years from now, is one more than twice his present age. Find his present age.
Solution
| Past Age | Present Age | Future Age |
| x-5 | x | x+7 |
(x-5) (x+7) = 2x + 1
x² + 2x -35 = 2x+1
x² - 36 = 0
x² = 36
x= +_ 6
Present Age- 6 years
Question 6 Two concentric circles are of radii 4 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution-

SECTION B
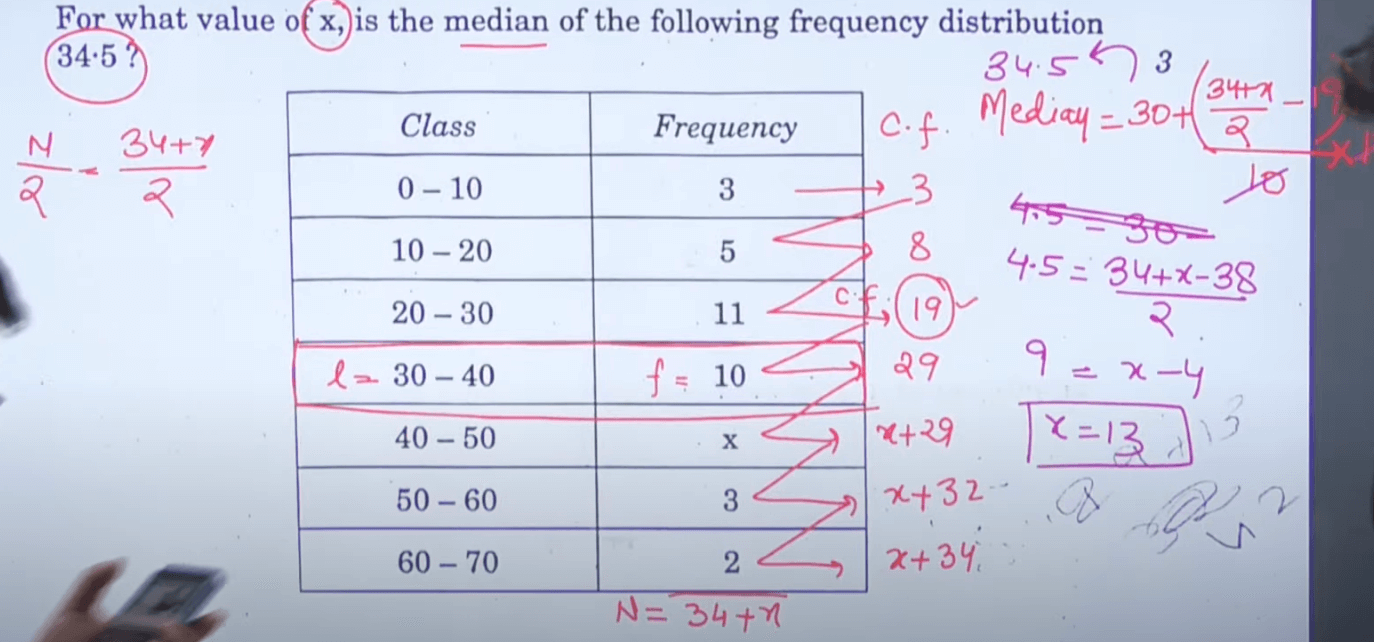
Question 7- For what value of x, is the median of the following frequency distribution 34:5?
| Class | Frequency |
| 0-10 | 3 |
| 10-20 | 5 |
| 20-30 | 11 |
| 30-40 | 10 |
| 40-50 | x |
| 50-60 | 3 |
| 60-70 | 2 |
Solution-
Question 8- Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Construct tangents to the circle from these two points P and Q.
Solution-

Question 9-
(a) The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building.
Solution-

tan 60° = 50/b
b= 50/ tan 60°
b = 50/ √3
b= 50√3 / 3
tan 30° = h/(50√3/3)
h= 50√3/3 x 1/√3
= 50/3 m= 16.67 metres
OR
(b) From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, then find the width of the river.
Solution-
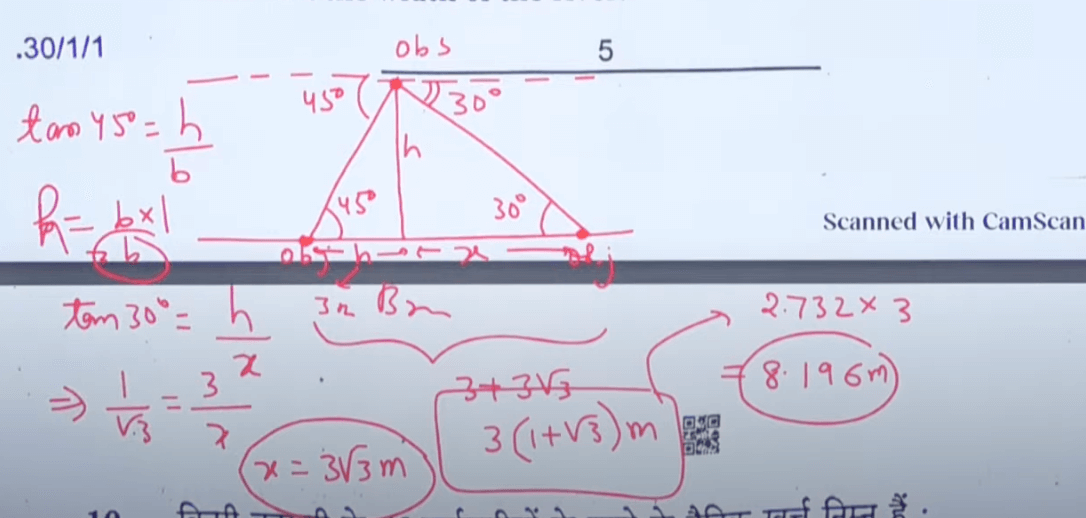
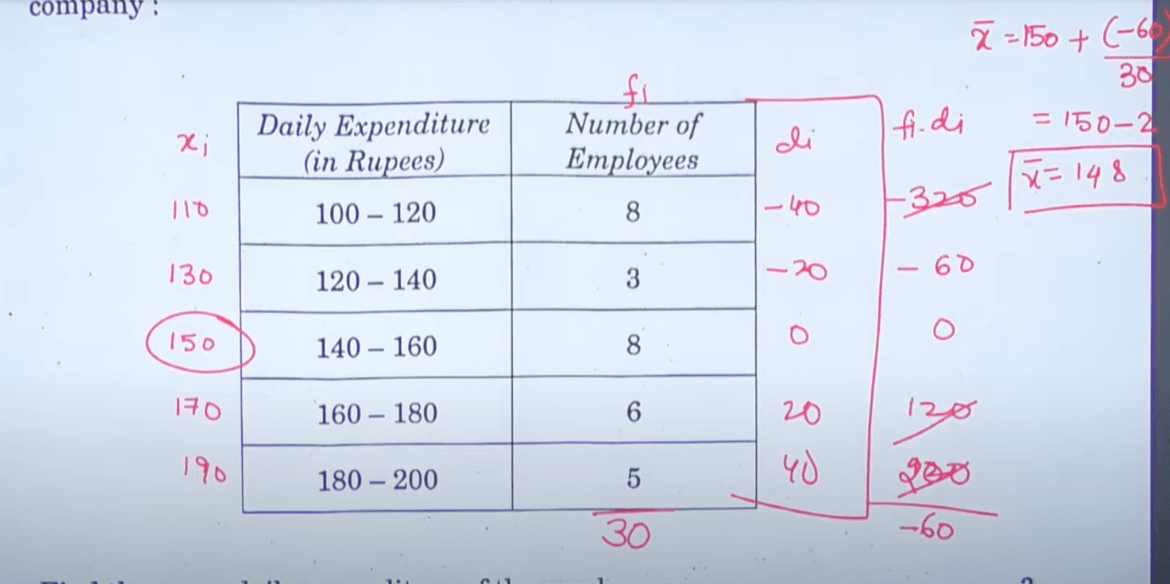
Question 10- Following is the daily expenditure on lunch by 30 employees of a company, Find the mean daily expenditure of the employees.
Solution
Question 11- From a solid cylinder of the height of 30 cm and radius of 7 cm, a conical cavity of height of 24 cm and same radius is hollowed out. Find the total surface area of the remaining solid.
Solution- H= 30 cm
R= 7 cm
Total Surface Area of Cylinder = Curved Surface Area of Cylinder + Curved Surface Area of Cone + πr²
TSA = 2 πrh + πrl + πr²
= πr (2h+ l+ r)
= 22/7 x 7 (60+25 + 7)
= 22 x 92
TSA= 2024 cm
OR
Water in a canal, 8 m wide and 6 m deep, is flowing with a speed of 12 km/hour. How much area will it irrigate in one hour, if 0.05 m. of standing water is required?
Solution- Flow Rate= 12 kmph
time= 1 hour
b= 8 m
h= 6m
lbh = LBH
lbh = Area x H
12x 8 x 6 x 1000 = Area x 5 /100
1152000 m² = Area
Question 12- In Figure 1, a triangle ABC with ㄥB = 90° is shown. Taking AB as diameter, a circle has been drawn intersecting AC at point P. Prove that the tangent drawn at point P bisects BC.
Class 10 Science Term 2 Sample Paper & Solution- Click to Check
CASE STUDY-1
Question 13- In Mathematics, relations can be expressed in various ways. The matchstick patterns are based on linear relations. Different strategies can be used to calculate the number of matchsticks used in different figures.
One such pattern is shown below. Observe the pattern and answer the following questions using Arithmetic Progression::
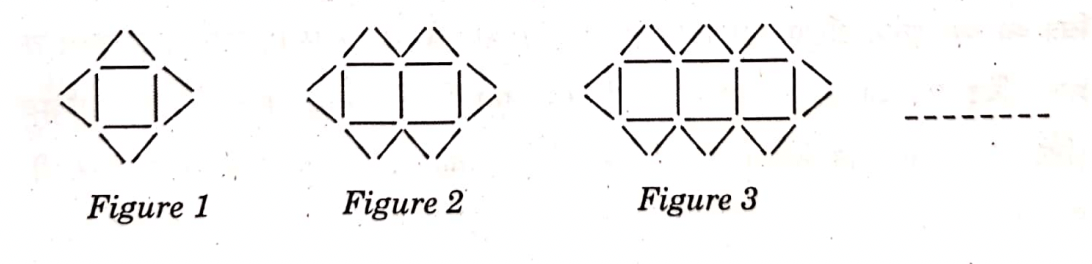
(a) Write the AP for the number of triangles used in the figures. Also, write the nth term of this AP. Which figure has 61 matchsticks?
Solution- AP = 4, 6, 8, 10
a= 4, d= 2
Tn = 4 + 2(n-1)
Tn= = 4 + 2n - 2
Tn= 2n +2
(b) Which figures has 61 matchstickes?
Solution- 12, 19, 26, …
Tn = 61
a + (n-1) d= 61
12 + 7(n-1) = 61
7(n-1) = 49
n-1 = 7
n= 8
8th figure has 61 matchsticks
Class 10 Maths Term 2 Question Paper PDF [Basic Maths]
Class 10 Maths Term 2 Question Paper PDF [Standard Maths]
Class 10 Maths Answer Key Term 2- Marking Scheme
As the pattern is new and so is the marking scheme for each question. Let's have a look at the section-wise CBSE Class 10 Maths Term 2 Marking Scheme to be followed by the CBSE.
For Basic Maths- Class 10 Term 2 Basic Maths Exam will consist of 14 questions divided into 3 sections A, B, C.
- Section A comprises 6 questions with 2 marks each
- Section B comprises 4 questions with 3 marks each
- Section C comprises 4 questions with 4 marks each
For Standard Maths- Class 10 Term 2 Standard Maths Exam will consist of 14 questions divided into 3 sections A, B, C.
- Section A comprises 6 questions with 2 marks each
- Section B comprises 4 questions with 3 marks each
- Section C comprises 4 questions with 4 marks each
