CBSE Class 12 Maths Answer Key 2023
CBSE Class 12 Maths Answer Key 2023: Board Class 12 Mathematics Exam 2023 has been scheduled for 11th March 2023 and lakhs of 12th Class students are to appear in the exam. As the exam is over, students must be rushing to know the correct responses to the Maths Questions asked in class 12 Maths board exam. We are providing the Answer Key of the Class 12 Maths Exam prepared by our expert faculty here so that the students can match their responses attempted in the exam. With the correct answers that are provided here, you can calculate how many marks can be expected in your board exam.
Class 12 Maths Answer Key 2023
If you had your Class 12 Maths Exam on 11th March 2023, then you must stay tuned with us so that you do not miss out on the updation of the Maths Class 12 Answer Key 2023 that is been discussed by our faculty. The students can cross-check their responses to all the questions they attempted in the exam to the answers that will be provided here. After this, the students can begin their studies for the next exams. For the satisfaction of students, we have provided an Unofficial answer key for Maths Class 12 here.
| Class 12 Maths Answer Key 2023 | |
| Exam Conducting Body | Central Board of Secondary Education |
| Class | CBSE Class 12 |
| Exam Name | Mathematics |
| Post Category | Answer Key |
| Level | Moderate & Calculative |
| Exam Date | 11th March 2023 |
| Unofficial CBSE Answer Key | 11th March 2023 |
| Official Website | https://www.cbse.nic.in/ |
Class 12 Maths Answer Key 2023 & Solution
Here, we have provided the complete Class 12 Maths Answer Key 2023 with correct answers one by one. So if are looking for the complete CBSE Class 12 Maths Answer Key go through the solutions that are discussed by our faculty in their live session. Connect with them and know the correct answers to the questions asked in today’s exam.
Class 12 Maths Answer Key & Question Paper 2023 (Set-2, 65/4/2)
The students who appeared in the Maths Class 12 Exam, can cross-check their Answer Key for Class 12 Maths Paper which will be provided here by our expert faculty. Stay tuned with us to get the correct responses to all the questions asked in today’s exam through this article.
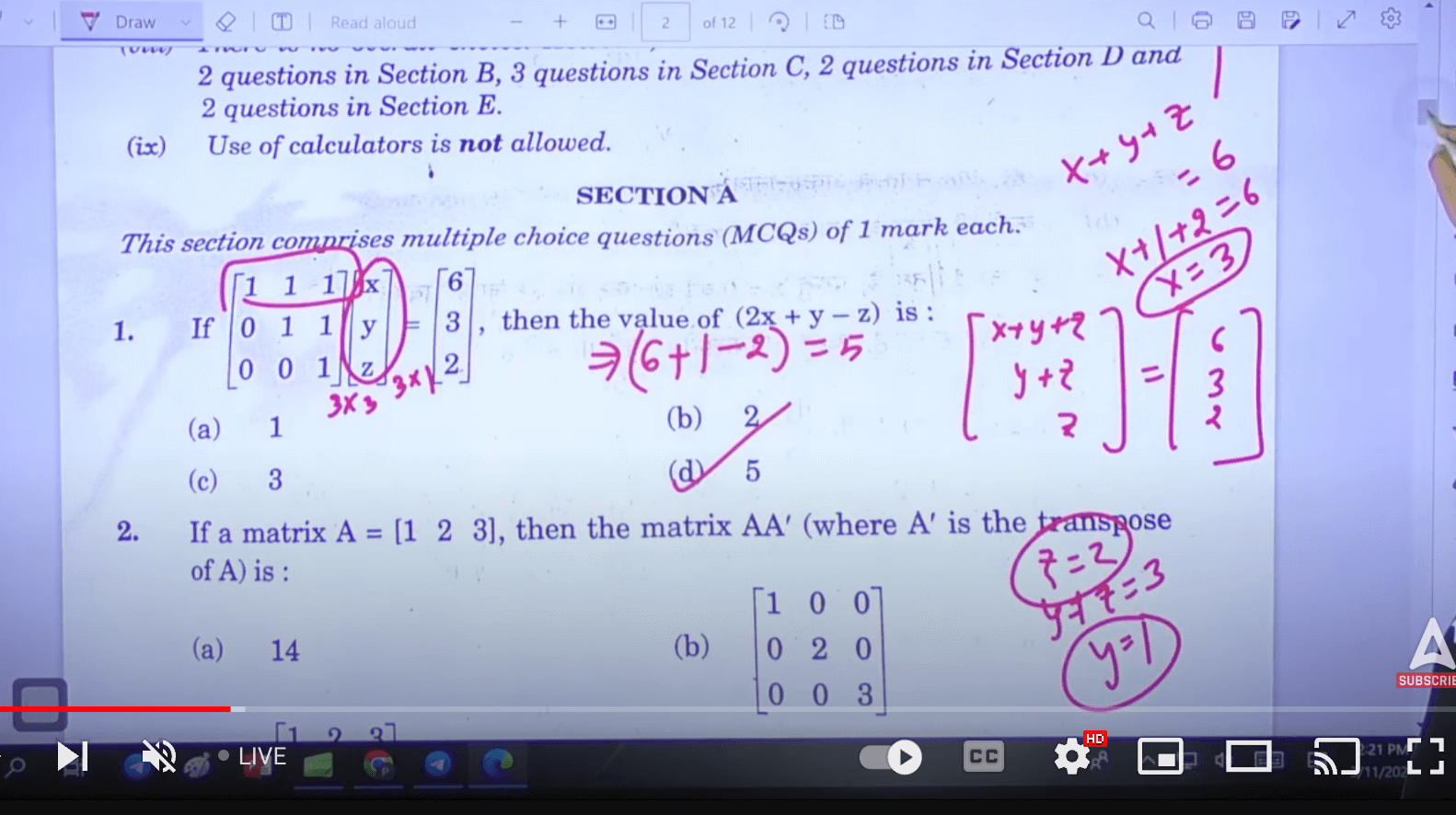
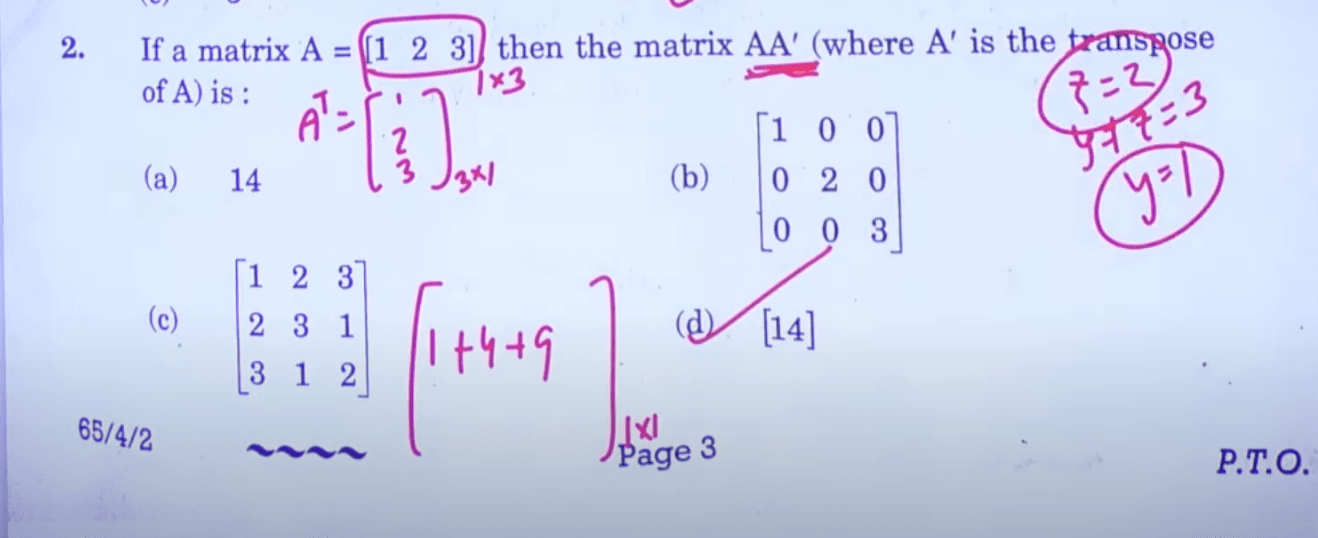
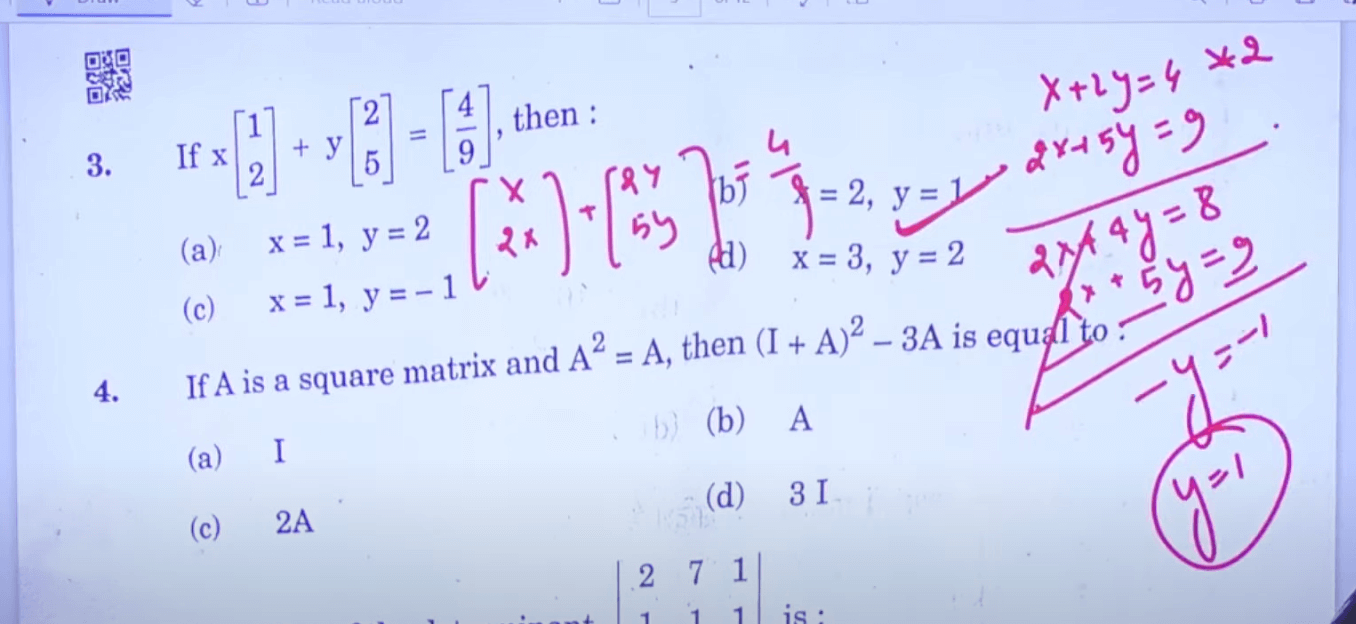
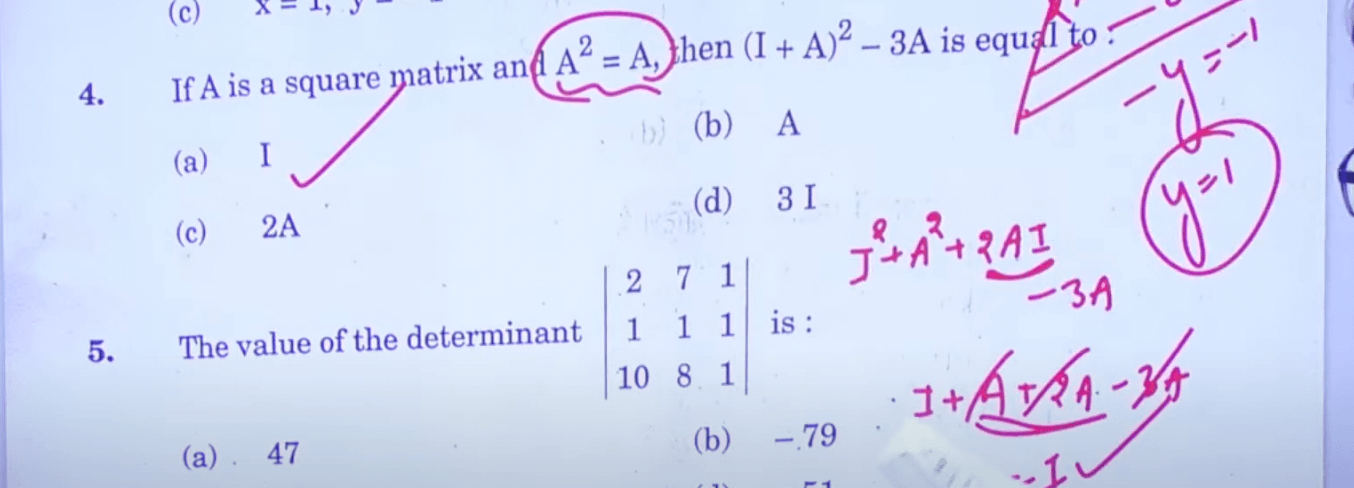

Class 12 Maths Question Paper 2023 Paper
CBSE has conducted Class 12 board exam and released different sets. Download Class 12 Math Question Paper 2023 pdfs for few sets from here and check questions asked in board exam.
Class 12 Maths Question Paper 2023 (Set 65-4-1) Download PDF
Class 12 Math Question Paper 2023 (Set 65-3-2) Download PDF
Class 12 Maths Question Paper 2023 (Set 65-3-3) Download PDF
Class 12 Maths Answer Key 2023 Scheme
As per the revised scheme of the Class 12th Board, CBSE had conducted the board exam and is now ready with the Class 12 Maths Exam. The CBSE board will follow the scheme of Maths Class 12 Exam Scheme as discussed below-
1. Section A has 18 MCQs and 02 Assertion-Reason-based questions of 1 mark each.
2. Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
3. Section C has 6 Short Answer (SA)-type questions of 3 marks each.
4. Section D has 4 Long Answer (LA)-type questions of 5 marks each.
5. Section E has 3 sources based/case based/passage based/integrated units of assessment (4 marks each) with sub-parts.




 Bihar Jeevika Result 2025-26 Out Soon at...
Bihar Jeevika Result 2025-26 Out Soon at...
 UPPSC Staff Nurse Syllabus 2026 and Exam...
UPPSC Staff Nurse Syllabus 2026 and Exam...
 UP SI Exam City 2026 Out, Check UPPRPB E...
UP SI Exam City 2026 Out, Check UPPRPB E...







