Differentiation Formula, Definition, Concept and Examples

Differentiation Formula, Definition, Concept, and Examples: In the study of calculus, Differentiation refers to the process of calculating the derivatives of a function. A derivative is defined as the rate of change of a particular function with regard to another function in mathematics or physics mainly. The eminent scientist, Isaac Newton, propounded the laws of Differential Calculus. The study of Differentiation and Integration makes the main concepts of calculus in mathematics. Many branches of science deal with the principles of limits and derivatives. In this article, you will know more about the definition of differentiation and derivatives, the rules of differentiation, and different formulas of differentiation to find the derivatives of algebraic functions, trigonometric functions, and exponential functions. These topics of differentiation are very useful for students of classes 11th and 12th as differentiation is mentioned in their syllabus.

What is Differentiation?

In calculus, the process of differentiation denotes the rate of change of one quantity with respect to another one. For example, the speed of a moving body is calculated as the rate of change in traveling distance vis-a-vis time. The calculated speed is the same as the slope which shows the instantaneous rate of change of the traveling distance over a time period. The differentiation process helps to calculate the rate of change of variable p with respect to q. The graph of q made against that of p is called the gradient of the curve. The differentiation means the ratio of a small change in a particular function with a small change in another function that relies on the first function. The larger or smaller value of a function or quantity like velocity, acceleration of moving objects, and tangent of a curve are calculated by the process of differentiation. When y is = f (x) that is differentiable then the differentiation process is expressed as f'(x) or dy / dx. 

What is Derivative?

The means of derivative y = f (x) geometrically is the slope of the tangent to the curve y = f(x) at ( x, f(x)). The computation of the derivative of a given function with the help of the limits is considered the first principle of differentiation. The derivative of a function is generally represented as d/dx. Suppose a function of a specific curve be y = f(x). Let us consider the P point with its coordinates (x, f(x)) on that curve. Let us consider another Q point with its coordinates (x+h, f(x+h)) on that curve. Now PQ becomes the secant line to the curve. The slope of the curve at a specific point refers to the slope of the tangent line at that point. We know that the slope of the secant line PQ is (y2−y1) / (x2−x1).

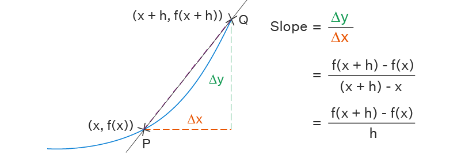
Hence,

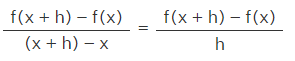
We need ‘h’ to be as less as possible to find the tangent slope. We know y = f(x). If the value of x is increased and denoted by Δx, then the value of y will also be increased and denoted by Δy.

So, y + Δy = f(x + Δx)

f(x) + Δy = f(x + Δx)

Δy = f(x + Δx) - f(x)

By dividing the above equation on both sides by Δx,

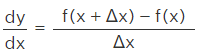
As the change is too small in value, applying the limits here

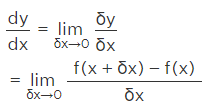
Here d/dx denotes the differential coefficient which is also called the Leibnitz symbol.

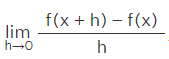
When the limits are applied, f'(x) is considered the first derivative of f(x). This process of finding the derivative of the given function is called differentiation.

The derivative is defined as when f is a real-valued function of a given real variable that is defined on an open interval I and if y = f(x) is a differentiable function of x then 

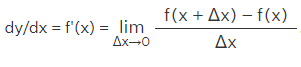
List of Differentiation Formula

Let us suppose that a function y = x^n , n > 0 then f(x + Δx) = (x + Δx)^n and f(x + Δx) - f(x) = (x + Δx)^n - x^n

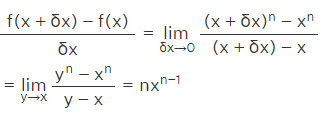
Here y = x + Δx and y → x as Δx → 0

In a similar way, we can extract the derivatives of other functions like algebraic, exponential, and trigonometric functions with the help of the basic rules of differentiation.

Differentiation Formula for Elementary Functions

The derivative formula helps to calculate the derivatives of the given functions and if the derivatives are of elementary functions then these are called the differentiation formulas.

1. The derivative of a constant function is 0: When y = k, where k is any constant term then y' = 0
2. The derivative of a power function: When y = xn , n > 0 then y' = n x n-1
3. The derivative of logarithmic functions: When y = ln x, then y' = 1 / x and when y = loga x, then y' = 1 / [(log a) x]
4. The derivative of an exponential function: When y = a x , then y’ = ax log a

Differentiation Formula for Trigonometric Functions

The concept of Trigonometry in mathematics shows the relationship between angles and sides of a given triangle. There are mainly six trigonometric ratios like sine, cosine, tangent, cotangent, secant, and cosecant. You should know the fundamental trigonometric formulas on the basis of these trigonometric ratios. Here the differentiation formulas for derivatives of trigonometric functions are given below.

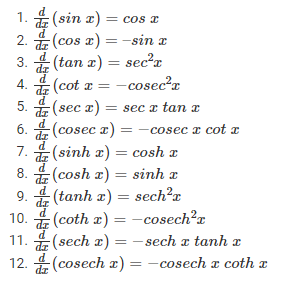
Differentiation Formula for Inverse Trigonometric Functions

The inverse of trigonometric ratios is considered the Inverse trigonometry function in mathematics. Here the differentiation formulas for derivatives of inverse trigonometric functions are given below.

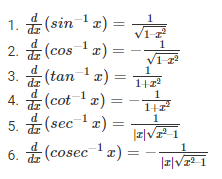
Differentiation Formula for Special Functions

When x= f(t), and y = g(t), where t is a quantity then we use the differentiation formula of that particular parametric function. 

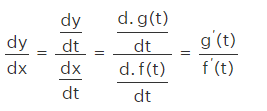
When y = f(x) and z = g(x), then the differentiation of y with regard to z is written as

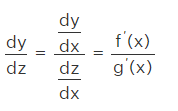
Differentiation Formula for Logarithmic Functions

When a given function is the product and quotient of that function, as expressed in y = (f1(x).f2(x).....) / (g1(x).g2(x)....), then we need to have the logarithm of that function and then differentiate it. When a function is given as an exponent of one function over another function, as expressed in [f(x)] g(x) then we need to take the logarithm of that function f(x) with its base e and then differentiate it. This is called the logarithmic differentiation process. 

Question: Differentiate the given function y = x^x .

Solution: If y = x^x then log y = x log x

1/y. dy / dx = log x + 1

dy / dx = y. (logx + 1) =  x^x (logx + 1)

Differentiation Formula for Implicit Functions

Suppose f(x,y) is a given function in the form of x and y. When we can’t find out directly for y, then we have to apply implicit differentiation. Imagine f(x,y) = 0 (Implicit function), then differentiate this function with regard to x and obtain the terms dy / dx at one side and calculate it further. 

Question: Find out dy/dx if x² +y² =1.

Solution: As we can’t derive the direct differentiation here so given function is considered the implicit function. Here we need to differentiate both sides of the equation.

d/dx. x² + d/dx. y² = d/dx.1

2x + 2y.dy/dx = 0

dy/ dx = -x/y

Differentiation Formula for High-order Derivation

We can calculate the higher-order derivatives on the successive processes of differentiation. The second differentiation of the obtained first derivative is written as f'' or d²y / dx² and the third derivative is written as f'" or d³y / dx³. The nth time of the derivative of f(x) is f n(x). For example, the rate of displacement change is called the velocity. The second derivative of displacement change is called the acceleration and its third derivative is considered the jerk.

Question: Find out the high-order differentiation of function y = f(x) = x⁵ - 3x⁴ + x

Solution: The first derivative is f'(x) = 5x⁴ - 12x³ + 1

The second derivative is f²(x) = 20x³ - 36 x²

The third derivative is f³(x) = 60x² - 72 x

The fourth derivative is f⁴(x) = 120x -72

Rules of Differentiation Process

When f is a differentiable function at a given point x = x₀, then f is called the continuous function at x₀. When a function is differentiable at every point of (a,b) then that function becomes differentiable in an interval of (a,b). The addition, subtraction, multiplication, and composite of differentiable functions, where these functions are defined, are considered differentiable functions. It is to be noted here that the quotient of 2 differentiable functions is also differentiable, wherever they are defined. The process of differentiation means that continuity but its reverse is not true in calculus. The differentiation rules are mentioned below.

1. Sum Rule: When y = u(x) ± v(x), then dy/dx = du/dx ± dv/dx
2. Product Rule: When y = u(x) × v(x), then dy/dx = u.dv/dx + v.du/dx
3. Quotient Rule: When y = u(x) ÷ v(x), then dy/dx = (v.du/dx- u.dv/dx)/ v²
4. Power Rule: When y = xn , then (d/dx) (xn) = nxn-1
5. Chain Rule: Suppose y = f(u) be a function of u and when u=g(x) so that y = f(g(x), then d/dx(f(g(x))= f'(g(x))g'(x)
6. Constant Rule: When y = k f(x), k ≠ 0, then d/dx(k(f(x)) = k d/dx f(x)

Differentiation Formula Examples

The problems of Differentiation with answers are given in the textbook of Class 11 and Class 12. Some differentiation questions with answers have been provided here below to know the concepts of differentiation easily.

Question 1: Solve out the differentiation of y = cos(tan x)

Solution: Given that the function y = cos(tan x)

Let us consider that u = tan x

y = cos u

By applying the chain rule of differentiation,

dy/dx = dy/du. du/dx

dy/dx = d(cos u) / du. d(tan x) / dx = -sin u . sec² x

dy/dx = -sin (tan x) . sec² x

Question 2: Compute the derivative of x / (1+tan⁡x) with the help of the differentiation rule.

Solution: Given that function y = x/ (1+tan⁡x)

We will differentiate the y function with regard to x.

This is in the form y' = u(x) / v(x)

By applying the quotient rule of the process of differentiation, 

As we know d/dx(u/v) = (v.u'- u.v') / v²

v = 1 + tan x and u = x

v' = sec²x and u' = 1

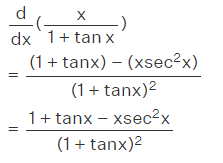
Question 3: Calculate the differentiation of the function y = x³ + 5 x² + 3x + 7.

Solution: Given that the function y = x³ + 5 x² + 3x + 7

By applying the differentiation formula of the power rule, 

we have dy/dx = dy / dx( x³ + 5 x²+ 3x + 7)

dy/dx = d(x³) / dx + d(5 x² ) / dx + d(3x) / dx + d(7) / dx

dy/dx = 3 x² + 5(2x) + 3 dy / dx + 0

dy/dx = 3 x² + 10 x + 3

Question 4: Find the Differentiation of x⁵ function with respect to x.

Solution: Given that function y = x⁵

By differentiating we have,

dy/dx = d(x⁵) / dx

y’ = 5x(⁵-') = 5x⁴

Hence d(x⁵) / dx = 5x⁴

Question 5: Find the Differentiation of function 10x² with respect to x. 

Solution: Given that function y = 10x²

y’ = d(10x²) / dx

y’ = 2.10.x = 20x

Hence d(10x²) / dx = 20 x

 Integration Formula for Class 12th- Click to Check