Volume of Cylinder- Formula, Questions and Answers

Volume of Cylinder: A cylinder could be explained as a three-dimensional shape having a circular base. In geometrical terms, a cylinder is a three-dimensional solid shape that consists of two parallel bases linked by a curved surface. Most bases look-alike circular disks. Some examples of cylinders are- pipes, batteries, barrels etc. In Mathematics, geometry is an important aspect where we have to learn the shapes and their properties of any 3d shape. In this article, we have discussed Volume of Cylinder, SA of Cylinder, and some solved questions to help you understand the concept in an appropriate manner. 

Volume of Cylinder

The volume of a cylinder is the capacity of the cylinder that calculates the amount of material quantity it can hold. The volume of the cylinder can be given by the product of the area of base and height. 

The formula for the Volume of a cylinder defines as,

Volume (v) = Area of base (A) X Height (H)

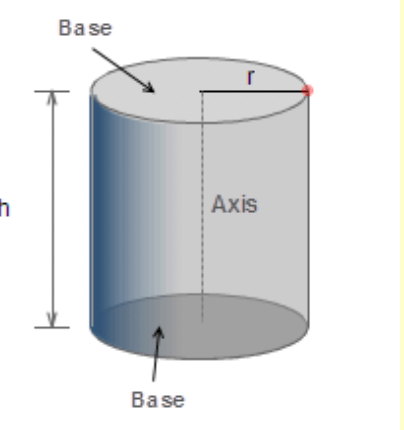
For any solid cylinder with a base radius ‘r’ and height of the cylinder is ‘h’

Therefore, the Volume of the cylinder is (V) = πr²h cube units.

Surface Area of Cylinder

The surface area of a cylinder can be defined as the curved surface area and the total space covered by the flat surfaces of the bases of the cylinder. SA of a cylinder could be written as-

The surface area of the Cylinder = Curved surface area + Area of both the circles

= ( Parameter of base X Height )+(2 × πr²)

= 2 πr× h + 2 πr²

= 2 πr (h + r)²

Volume of Hollow Cylinder

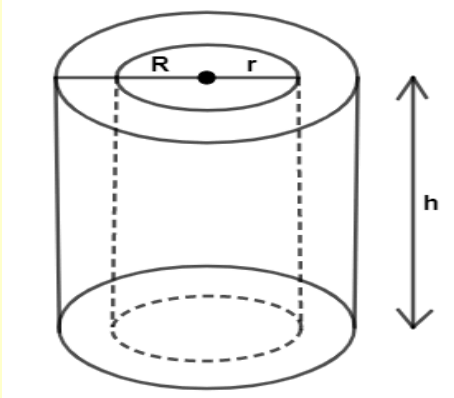
The hollow cylinder is a cylinder, which is empty from the inside having some difference between the internal radius and external radius. The bottom of the hollow cylinder resembles an annular ring. For any hollow Cylinder with height ‘h’, external Radius ‘R’ and internal Radius ‘r’. So. Thickness = (R-r).

Therefore,

Volume of the hollow cylinder is (V) = π(R²-r²)h cubic units.

Surface area of the Cylinder= Curved surface area + Area of both the circles

= 2πh(R + r) + 2π(R²-r²) square units.

Problems Based on Volume of Cylinder

Q1. Find the volume of a cylindrical water tank whose base radius is 25 inches and whose height is 120 inches. (pi- 3.14)

a) 235600 cubic inches 

b) 235500 cubic inches

c) 22570 cubic inches 

d) None of those

Solution:

The base radius of the given cylinder is 25 inches.

Its height is 120 inches

Using the formula of the cylinder, the volume of the tank is

V = πr²h

V= (3.14)×(25)²×120

=235500 cubic inches.

So, correct answer is option (b)

Q2. Calculate the radius of the base of a cylindrical container of volume 440 cm³. Height of the cylindrical container is 35 cm. (Take pi = 22/7)

a) 4 cm 

b) 2 cm 

c) 3 cm 

d) None of those

Solution:

Given:

Volume = 440 cm³ , Height = 35 cm

We know from the formula of cylinder;

Volume, V = πr²h cubic units

So, 440 = (22/7) × r² × 35

r²= (440 × 7)/(22 × 35) = 3080/770 = 4

Therefore, r = 2 cm

Q3. The height of a cylindrical pillar is 15 m. The diameter of its base is 350 cm. What will be the cost of painting the curved surface of the pillar at Rs 25 per m²?

a)Rs. 4125 

b) Rs.4000 

c) Rs. 3900 

d) None of those

Solution-

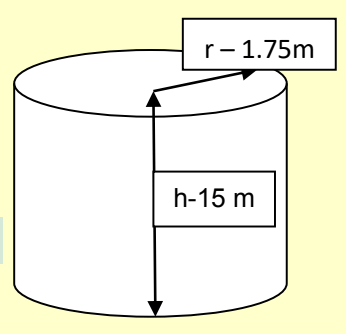
The base is circular and so the pillar is a right circular cylinder.

Here, if diameter is 350 cm than radius = 175 cm = 1.75 m and height = 15 m

Therefore, the curved surface area of the pillar = 2πrh

= 2 × (22÷7)× 1.75 × 15 m²

= 165 m²

Therefore, the cost of painting this area = Rs 25 × 165 = Rs 4125.

So, Answer (a)

Q4. A drainage tile is a cylindrical shell 21 cm long. The inside and outside diameters are 4.5 cm and 5.1 cm respectively. What is

the volume of the clay required for the tile?

a) 6.96π cm³ 

b) 6.76π cm³

c) 5.76π cm³ 

d) None of the above

Solution-

Inner radius r = 4.5/2 cm = 9/4 cm

Outer radius R = 5.1/2 cm = 51/20 cm

Height h = 21 cm

Volume = π(R + r) (R - r)h

= π x[(51÷20)+(45÷20)]x[(51÷20)–(45÷20)]x 21

= π x(96÷20)x(6÷20)× 21

= 30.24 π cm³ (Answer)

Q5. What is the height of a solid cylinder of radius 5 cm and total surface area is 660 cm²?

a) 10 cm 

b) 12 cm 

c) 15 cm 

d) 16 cm

Solution-

Total surface area of a cylinder = 2Πr(h + r)

⇒ [2 x 22 x 5 x (5 + h)]/7 = 660

⇒ 220 x (5 + h) = 660 x 7 cm

⇒ 5 + h = 21

or h = 16 cm

So, Answer (d)

Q6. A cylindrical tank 7 m in diameter, contains water to a depth of 4m. What is the total area of wetted surfaces?

a) 110 m²

b) 126.5 m²

c) 131.5 m²

d) 136.5 m²

Solution: 

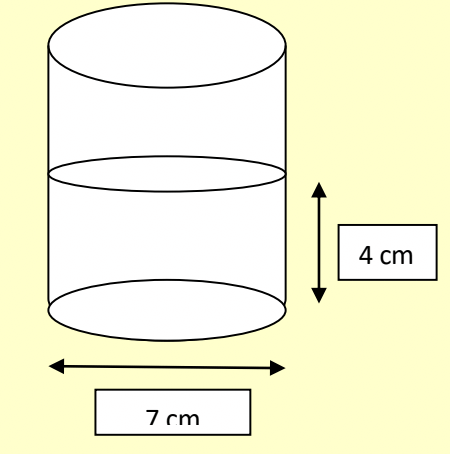
Wet surface = curved surface upto water level + bottom circle

Radius of the cylinder( r) = 7/2

Height of the cylinder( h) = 4

Area of wetted surface = Curved surface area of the cylinder + Area of base circle

= 2πrh + πr²

⇒ πr(2h + r)

⇒ (22÷7)×(7÷2)×[ 2 ×4 +(7÷2)}

⇒ 11 ×11.5

= 126.5 m²

Answer (b)