Trigonometry Table
A trigonometry table is a collection of the values of trigonometric functions for the commonly used standard angles 0°, 30°, 45°, 60°, 90° and non-standard angles 180°, 270° and 360°. Trigonometry is a topic and chapter in Mathematics, which involves the study of the relationship involving the length and angles of a triangle. Trigonometry plays a major role in class 10th, 11th and 12th mathematics subjects and in many competitive examinations some questions are asked from Trigonometry. Before going to learn Trigonometry you have to memorise the trigonometry table which is discussed below.
Trigonometry Table 0° to 360°
The trigonometric ratios table helps to find the values of trigonometric usual angles such as 0°, 30°, 45°, 60° and 90° as well as unusual angles such as 180°, 270°, and 360°. It consists of trigonometric ratios. The six trigonometric ratios are sine, cosine, tangent, cotangent, cosecant, and secant. These ratios can be written in short as sin, cos, tan, cosec, sec and cot. The values of trigonometric ratios of standard angles are essential to solve the trigonometry problems in classes 10th, 11th 12th and in any competitive exams. Therefore, it is necessary to remember the values of the trigonometric ratios from 0° to 360°. Let's have a look at the trigonometry table and function values from 0° to 360°.
| Trigonometry Table | ||||||||
|---|---|---|---|---|---|---|---|---|
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Trigonometry Table Tricks
Remembering the trigonometry table will help you to solve trigonometry questions and it is very easy to remember the trigonometry table for standard angles from 0° to 90°. If you know the trigonometry formula then remembering the trigonometry table is very easy. The Trigonometry ratios table is dependent upon the trigonometry formulas. Here, we are providing some trigonometry table tricks and formulas which are discussed below.
- sin (90°− θ) = cos θ
- cos (90°− θ) = sin θ
- tan (90°− θ) = cot θ
- cot (90°− θ) = tan θ
- cosec (90°− θ) = sec θ
- sec (90°− θ) = cosec θ
- 1/sin θ = cosec θ
- 1/cos θ = sec θ
- 1/tan θ = cot θ
Trigonometry Table Chart
The values of trigonometric functions for the angles 0°, 30°, 45°, 60°, and 90° in a trigonometry table are commonly used to solve trigonometry problems and questions. Thus, 0°, 30°, 45°, 60°, and 90° are called the standard angles. The trigonometry table chart for standard angels is given below. you can download the Trigonometry Table chart for future use and to learn trigonometry Table values.
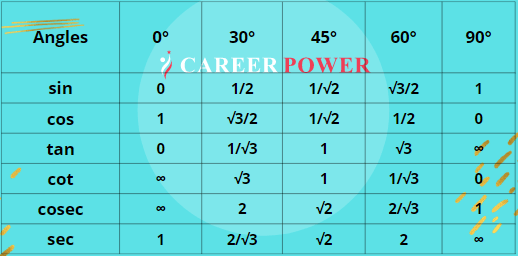
Trigonometry Table for Trigonometric Functions
There are six trigonometric functions in trigonometry which are Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent. It is also known as sin, cos, tan, cosec, sec and cot. The trigonometry table for each trigonometric function is discussed below.
Trigonometry Table for sin
The trigonometry table for the sin function is given below. The value of sin0° is 0 and the value of sin 90° is 1. The value of sin 30° is 1/2 and the value sin 45° is 1/√2.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Trigonometry Table for cos
The trigonometry table for the cos function is given below. The value of cos 0° is 1 and the value of cos 90° is 0. It is just the opposite of sin function from 0° to 90°.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
Trigonometry Table for tan
The trigonometry table for the tan function is given below. The value of tan 30° is 1/√3 and the value of tan 60° is √3.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Trigonometry Table for cot
The trigonometry table for the cot function is given below. The value of cot 30° is √3 and the value of cot 60° is 1/√3.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
Trigonometry Table for cosec
The trigonometry table for the cosec function is discussed below. The value of cosec 45° is √2 and the value of cosec 30° is 2.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Trigonometry Table for sec
The trigonometry table for the sec function is discussed below. The value of sec 45° is √2 and the value of sec 30° is 2. The value of sec 0° is 1.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Examples Related Trigonometry Table
Q1. If the value of sin A is given to be 0.66 at 40° then at which angle again the sin A will be equal to 0.66?
Solution: As we know sin repeats its value after 360°.
So from this property, we can conclude that
sin A will have the same value at 40 + 360 = 400°
Hence, at 400°, the sin A will again be equal to 0.66
Q2. What is the lowest value of the angle (in radians) at which sin A is equal to cos A?
Solution: The value of sin A and cos A becomes equal at 45°, that is at Π/4. After this value, they are equal after every 360° interval of Π/4.
Q3. It is given that tan is 0.72 at a certain angle x. What will be the value of cot at this angle?
Solution: As we know, tan = 1/cot
So, the value of cot x = 1/tan x
So, tan x = 1/0.72
Q4. If sin(A+B) = 1/2 and sin(A-B) = 1/√2, then find the value of A and B in degrees.
Solution: Given, sin(A+B) = 1/2
As sin 30° = 1/2
Hence, sin(A+B) = sin 30°
Or, A+B = 30 ---------- (i)
sin(A-B) = 1/√2
As, sin 45° = 1/√2
sin(A-B) = sin 45°
So, A-B = 45° ---------------(ii)
On adding equation (i) and (ii), we get
(A+B) + (A-B) = 30° + 45°
2A = 75°
A = 75/2°
A = 37.5°
Putting the value of A in equation (i)
37.5° + B = 30°
B = 30° - 37.5°
Hence, B = -7.5°
| Related Links | |
|---|---|
| Even Numbers | Composite Numbers |
| Roman Numbers | Tables 2 to 20 |
| Mensuration Formulas | Prime Numbers |
| Natural Numbers | Rational Numbers |
| Odd Numbers | Co Prime Numbers |
