Trigonometry Formulas and Identities, All Formula List

Trigonometry is one of the most important topics in mathematics to learn for Class 10 to 12 students and for the students who are preparing for entrance examinations JEE Main, JEE Advanced etc. Trigonometry involves various types of problems that we can solve with special math tools called trigonometric formulas and identities. But using these tools correctly is important for finding the right answers. In this article, we are providing all basic and advanced Trigonometry formulas for Classes 10, 11, and 12.

Trigonometry Formula

Trigonometry deals with the relationships between the angles and sides of triangles where “Trigon” means triangle and “metry” means measurement. Trigonometry formulas provide the facility to solve complex problems involving angles, distances, and other geometric concepts. This article includes all trigonometry formulas including the trigonometry table with function values. These trigonometry formulas will help the students of Class 10th, 11th, and 12th to score good marks in mathematics subject.

Trigonometry Table

Before getting into trigonometry maths formulas, it’s important to understand what the trigonometry table itself means. The word “trigonometry” has two parts: “trigon,” which means triangle, and “metry,” which means measurement. So, trigonometry is basically about measuring and understanding triangles better. Here’s the chart of commonly used angle formulas in trigonometry to help solve problems.

Trigonometry Table
Angles	0°	30°	45°	60°	90°	180°	270°	360°
Radians	0	π/6	π/4	π/3	π/2	π	3π/2	2π
sin	0	1/2	1/√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1
tan	0	1/√3	1	√3	∞	0	∞	0
cot	∞	√3	1	1/√3	0	∞	0	∞
cosec	∞	2	√2	2/√3	1	∞	-1	∞
sec	1	2/√3	√2	2	∞	-1	∞	1

Trigonometric Ratios

Trigonometry ratios relate angles and sides in triangles. Sine (sin) is opposite/hypotenuse, cosine (cos) is adjacent/hypotenuse, and tangent (tan) is opposite/adjacent. They help solve triangle problems and model wave phenomena in various fields, like physics and engineering. Let’s have a look at the Trigonometric ratios for Right Triangle.

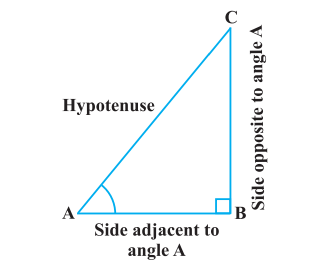
Basic Trigonometry Functions Formula

The 6 basic trigonometric functions are sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). Here are trigonometric functions, identities, and some basic formulas:

• sin θ = Opposite Side/Hypotenuse
• cos θ = Adjacent Side/Hypotenuse
• tan θ = Opposite Side/Adjacent Side
• sec θ = Hypotenuse/Adjacent Side
• cosec θ = Hypotenuse/Opposite Side
• cot θ = Adjacent Side/Opposite Side

Trigonometric Ratios for Unit Circle

Trigonometric ratios on the unit circle involve angles and coordinates. Sine (sin) is the y-coordinate, cosine (cos) is the x-coordinate, and tangent (tan) is sin/cos. They provide insights into circular motion, periodic functions, and complex numbers, crucial in mathematics, physics, and engineering.

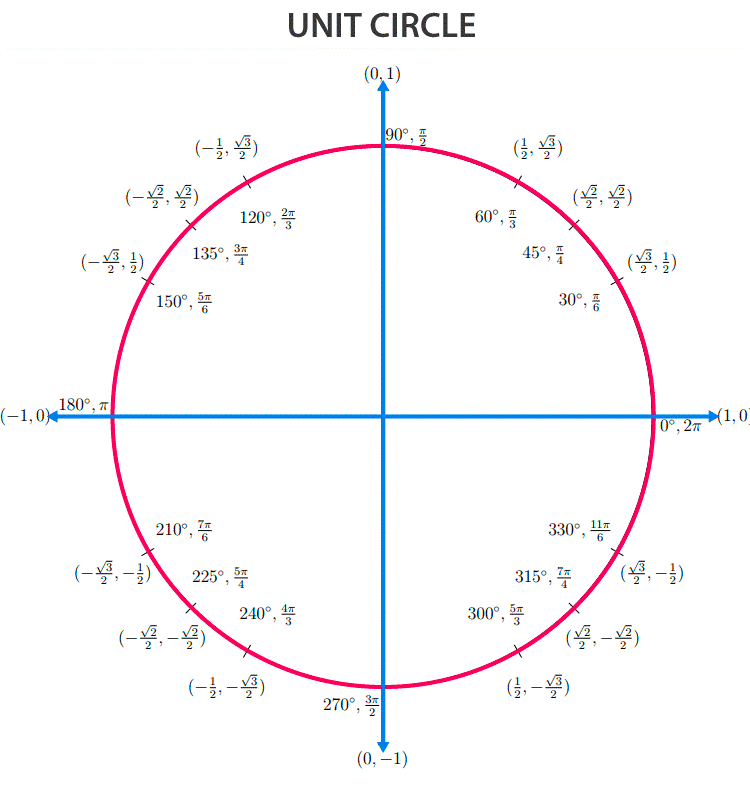
Generally, for a unit circle, the radius equals 1, and θ is the angle. The value of the hypotenuse and adjacent side here is equal to the radius of the unit circle.

Hypotenuse = Adjacent side to θ = 1

Therefore, the ratios of trigonometry are given by:

• sin θ = y/1 = y
• cos θ = x/1 = x
• tan θ = y/x
• cot θ = x/y
• sec θ = 1/x
• cosec θ = 1/y

Trigonometry Identities

Trigonometry identities are fundamental equations that establish relationships among trigonometric functions. These equations hold true for all angles and help simplify expressions and solve equations involving trigonometric functions. Trigonometry has different tricks called “identities” that help solve tricky problems. These identity tools make solving tough trigonometry questions easier and faster. Let’s explore some important ones together.

Reciprocal and Quotient Identities

Reciprocal and Quotient Identities provide relationships between the trigonometric functions which are discussed below.

Reciprocal Identities

Cosecant (cosec) is 1/sin, Secant (sec) is 1/cos, and Cotangent (cot) is 1/tan. These relationships link trigonometric functions and their reciprocals, helping simplify expressions and solve equations in trigonometry.

• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ
• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ

Quotient Identities

Tangent Identity tan θ = sin θ / cos θ  and Cotangent Identity cot θ = 1 / tan θ (cos θ / sin θ), provide connections between tangent, cotangent, sine, and cosine functions.

• $\tan \theta =\frac{\sin \theta }{\cos \theta }$
• $cot\theta =\frac{\cos \theta }{\sin \theta }$

Ranges of the Trigonometric Functions

The ranges of the trigonometry function sine, cosine, tangent, cotangent, secant and cosecant are as follows:

• −1 ≤ sin θ ≤ 1
• −1 ≤ cos θ ≤ 1
• −∞ ≤ tan θ ≤ ∞
• csc θ ≥ 1 and csc θ ≤ −1
• sec θ ≥ 1 sec θ ≤ −1
• −∞ ≤ cot θ ≤ ∞

Pythagorean Identities

The Pythagorean theorem lays the foundation for Pythagorean identities in Trigonometry, which relate to the trigonometric functions of an angle in a right triangle. Pythagorean Theorem states that, In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Pythagorean identity relates the sine and cosine functions of an angle.

Pythagorean identities state that sin²θ + cos²θ = 1 and csc²θ – cot²θ = 1, connecting trig functions in a right angle triangle. These fundamental equations are used extensively in trigonometry to establish relationships between sine, cosine, secant, cosecant, and cotangent.

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Even and Odd Angle Formulas

• sin(-θ) = -sinθ
• cos(-θ) = cosθ
• tan(-θ) = -tanθ
• cot(-θ) = -cotθ
• sec(-θ) = secθ
• cosec(-θ) = -cosecθ

Co-function Formulas

• sin(90°-θ) = cos θ
• cos(90°-θ) = sin θ
• tan(90°-θ) = cot θ
• cot(90°-θ) = tan θ
• sec(90°-θ) = cosec θ
• cosec(90°-θ) = sec θ

Sum & Difference Identities

• sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
• cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
• sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
• cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
• $\tan (a+b)=\frac{\tan a+\tan b}{1–\tan a.\tan b}$
• $\tan (a–b)=\frac{\tan a–\tan b}{1+\tan a.\tan b}$

Double Angle Formulas

• sin (2θ) = 2sinθ cosθ
  = 2tanθ/1+tan²θ
• cos (2θ) = cos²θ – sin²θ
  = 2cos²θ – 1
  = 1 – 2sin²θ
• tan2θ = 2 tanθ / 1-tan²θ

Half Angle Formulas

• $\sin \frac{\theta }{2} = \pm \frac{\sqrt{1+\cos \theta }}{2}$
• $\cos \frac{\theta }{2} = \pm \frac{\sqrt{1+\cos \theta }}{2}$
• $\tan \frac{\theta }{2} = \pm \frac{\sqrt{1–\cos \theta }}{\sqrt{1+\cos \theta }}$

Triple Angle Formulas

• sin 3θ = 3sinθ – 4sin³θ
• cos 3θ = 4cos³θ – 3cosθ
• $\tan 3\theta =\frac{(3\tan \theta –{\tan }^3\theta )}{1–3{\tan }^2\theta }$

Product to Sum Formulas

• sin a sin b = 1/2 [cos (a-b) – cos (a+b)]
• cos a cos b = 1/2 [cos (a+b) + cos (a-b)]
• sin a cos b = 1/2 [sin (a+b) + sin (a-b)]
• cos a sin b = 1/2 [sin (a+b) – sin (a-b)]

Angle Sum and Difference Formulas

Angle Sum and Difference Formulas are also known as sum Product Formulas. These formulas allow you to express the trigonometric functions of sums and differences of angles.

Sum of Angles Formulas:

• $\sin a + \sin b = 2 \sin \frac{a+b}{2} \cos \frac{a–b}{2}$
• $\cos a + \cos b = 2 \cos \frac{a+b}{2} \cos \frac{a–b}{2}$

Difference of Angles Formulas:

• $\sin a – \sin b = 2 \cos \frac{a+b}{2} \sin \frac{a–b}{2}$
• $\cos a – \cos b = –2 \sin \frac{a+b}{2} \sin \frac{a–b}{2}$

Periodic Formulas

If n is an integer, then
sin(θ + 2πn) = sin θ
cos(θ + 2πn) = cos θ
tan(θ + πn) = tan θ
cosec(θ + 2πn) = cosec θ
sec(θ + 2πn) = sec θ
cot(θ + πn) = cot θ

Inverse Trigonometry Formulas and Functions

Inverse trigonometric formulas are like special rules in math that help us figure out angles and values by using inverse trigonometric functions. We also call them inverse trigonometric identities. These functions are used to find angles given specific ratios of sides in a right triangle.

Inverse Trigonometric Functions

If Sin θ = x, then θ = sin^-1 x = arcsin(x)

Similarly,

θ = cos^-1x = arccos(x)

θ = tan^-1 x = arctan(x)

Also, the inverse properties could be defined as;

sin^-1(sin θ) = θ

cos^-1(cos θ) = θ

tan^-1(tan θ) = θ

Inverse Trigonometry Formulas

Inverse Trigonometry Formulas are tools in math that let us find angles and values using inverse trigonometric functions, also known as reverse trigonometry functions.

• sin^-1 (–x) = – sin^-1 x
• cos^-1 (–x) = π – cos^-1 x
• tan^-1 (–x) = – tan^-1 x
• cosec^-1 (–x) = – cosec^-1 x
• sec^-1 (–x) = π – sec^-1 x
• cot^-1 (–x) = π – cot^-1 x

Degrees to Radians Formulas

If x is an angle in degrees and t is an angle in radians then:

π⁄180° = t⁄x ⇒ t = πx/180° and x = 180°t⁄x

Law of Sines Cosines and Tangents

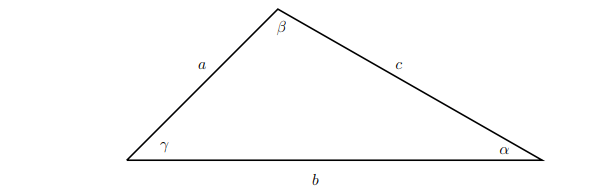
Law of Sines

The Law of Sines relates the ratios of a triangle’s side lengths to the sines of its angles, stating that the sine of an angle divided by the length of the opposite side is constant for all angles in the triangle

sin α/a = sinβ/b = sin γ/c

Law of Cosines

The Law of Cosines is a trigonometric formula used to find the lengths of sides in non-right triangles, relating the square of a side to the sum of the squares of the other two sides minus twice the product of their lengths and the cosine of the included angle.

a² = b² + c² − 2bc cos α
b² = a² + c² − 2ac cos β
c² = a² + b² − 2ab cos γ

Law of Tangents

a − b/a + b = tan½(α − β)/tan½(α + β)

b – c/ b + c = tan½ (β − γ)/tan½(β + γ)

a – c/ a + c = tan½ (α − γ)/tan½(α + γ)

Examples Related Trigonometry Formulas

Question 1: What will be the value of sinAcosA if it is given that the value of sin2A is 1/2?

Solution: As we know sin2A = 2sinAcosA

Given, sin2A = 1/2

Putting the value of sin2A on the LHS

2sinAcosA = 1/2

sinAcosA = (1/2) x (1/2)

Hence, sinAcosA = 1/4 

 

Question 2: It has been given that the value of sin2A is 1. Find out the value of (sinA – cosA).

Solution: Given, sin2A = 1 

As we know, sin2A = 2sinAcosA

We have to find the value of sinA – cosA

On squaring (sinA – cosA), we get (sinA – cosA)²

sin2A + cos2A – 2sinAcosA

As sin2A + cos2A = 1

and 2sinAcosA = sin2A

Substituting these values in the above equation, we get => 1 – sin2A

As given sin2A = 1

=> 1-1 = 0 

As, (sinA – cosA)2 = 0

sin A – cos A = √0

Hence, sinA – cosA = 0

 

Question 3: In a right-angle triangle ABC with side AC as hypotenuse, the value of sin A is given to be 1/2. What will be the value of cos C.

Solution: Given ABC is a right-angled triangle.

AC is given to be hypotenuse, so, B must be the angle with value 90°.

Given, sin A = 1/2 

As sin 30° = 1/2

So, sinA = sin30

Or, A = 30°

So, C must be 90° – 30° = 60°

Hence, cos C = cos60 = 1/2

So, the value of cos C =  1/2 

 

Question 4: Find the principal value of cos^–1x, for x=√3/2.

Solution: If cos^–1(√3/2) = θ, then cos θ = √3/2.

Since we are considering the principal branch, θ ∈ [0 , π]. Also, since √3/2 > 0, θ being in the first quadrant,

hence cos^–1 (√3/2) = π/6.

 

Question 5: Given a right-angled triangle with an angle θ where the opposite side is 5 units and the hypotenuse is 13 units. Find the values of sine, cosine, and tangent of θ.

Solution:

sin θ = Opposite/Hypotenuse = 5/13

cos θ = Adjacent/Hypotenuse = √ (13² -5²)/ 13 = √144/13 = 12/13

tan θ = Opposite/Adjacent = 5/12

 

Question 6: Solve the problem sin (𝛼+𝛽):  sin α = 3/5 and cos β =4/5

Solution: Given sin α = 3/5 and cos β =4/5

To find sin (𝛼+𝛽), use the angle sum identity:

sin (𝛼+𝛽) = sin𝛼 cos𝛽 + cos𝛼 sin𝛽

First, find cos 𝛼:

cos𝛼 = √1- sin²𝛼 = √1-(3/5)² = √16/5 = 4/5

Second, find sin 𝛽:

sin𝛽 = √1- cos²𝛽 = √1-(4/5)²= √9/25 = 3/5

Now substitute sin ⁡ 𝛼 sinα, cos ⁡ 𝛽 cosβ, cos ⁡ 𝛼 cosα, and sin ⁡ 𝛽 sinβ into the formula:

sin (𝛼 + 𝛽) = sin 𝛼 cos 𝛽 + cos 𝛼 sin ⁡𝛽

sin ⁡(𝛼+𝛽) = (3/5) (4/5) + (4/5) (3/5)

sin (𝛼+𝛽) = 12/25 + 12/25

sin⁡ (𝛼+𝛽) = 25/12 ​ + 25/12 ​

sin⁡ (𝛼+𝛽) = 24/25

Sharing is caring!