Right Angle Triangle: Definition, Properties and Formula

A triangle is a three-sided polygon. A Right Angle Triangle is a specific type of triangle with one angle measuring 90 degrees, called the right angle. The side opposite the right angle is the longest side, known as the hypotenuse, while the other two sides are called base and perpendicular.

Right Angle Triangle Definition (समकोण त्रिभुज)

A Right Angle Triangle is a shape with three sides where one corner is a 90-degree angle, which is a square corner. The side that’s opposite this corner is called the longest side. The other two sides are connected to this corner and meet at the square corner. This special triangle follows a rule called the Pythagorean theorem that helps us figure out how long the sides are.

If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triplet.

AB² = AC² + BC²

Pythagoras theorem: c² = b² + a²

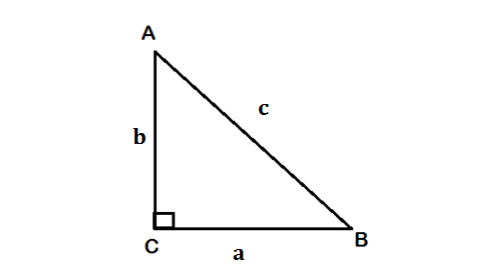
The side opposite the right angle is called the hypotenuse (side ‘c’ in the figure). The sides adjacent to the right angle are called legs. Side ‘a’ may be identified as the side adjacent to angle B and opposed to (or opposite) angle A, while side b is the side adjacent to angle A and opposed to angle B.

Properties of Right Angle Triangle

A Right Angle Triangle has one angle of 90 degrees, called the right angle. The Pythagorean theorem connects its sides: the sum of the squares of the shorter sides equals the square of the hypotenuse. It serves as a basis for trigonometry and has applications in various fields.

Certainly, here are the properties of a Right Angle Triangle presented in points:

1. One angle is exactly 90 degrees (the right angle).
2. The Pythagorean theorem relates the lengths of its sides: a² + b² = c².
3. Trigonometric ratios (sine, cosine, tangent) are based on their angles.
4. Special right triangles (45-45-90, 30-60-90) have specific side ratios.
5. Drawing an altitude from the right angle creates two similar triangles.
6. Its sides are perpendicular (meet at 90-degree angles).
7. The converse of the Pythagorean theorem helps identify right triangles.
8. The geometric mean theorem relates the lengths of segments on the hypotenuse.

Right Angle Triangle Diagram

A Right Angle Triangle is a triangle in which one angle is a 90-degree angle. In a right Angle Triangle, the sides are commonly labeled as Hypotenuse, Base and Perpendicular:

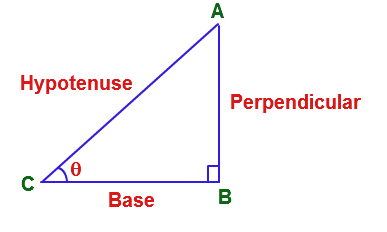
Hypotenuse: The hypotenuse is the longest side of the right triangle. It’s the side opposite the right angle. Think of it as the diagonal connecting the two other sides. The hypotenuse is represented by (c) in the Pythagorean theorem.

Base: One of the shorter sides of the right triangle. It’s the side adjacent to the right angle. The base forms the horizontal side of the triangle. The Base is represented by (a).

Perpendicular: The other shorter side of the right triangle. It’s also adjacent to the right angle. The side representing the perpendicular is denoted by (b) beneath the figure. The perpendicular stands vertically from the base, forming the right angle.

Right Angle Triangle Formula

(1) Pythagoras’s theorem is a fundamental principle in geometry that describes the relationship between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b).

in symbols: Hypotenuse² = Perpendicular² * Base²

(2) Are of a Right Triangle Formula: The formula for calculating the area (A) of a right triangle is:

Area of a Right Angle Triangle = ½ (Base × Perpendicular)

(3) The Perimeter of a Right Angle Triangle Formula

The formula for calculating the perimeter (P) of a right triangle is:

P = Base + Perpendicular + Hypotenuse

Sharing is caring!