What is the Factorial of 100?

Table of Contents

The definition of factorial can be said as integer ‘n’ which is either equal to or more than 0. The symbol of factorial is indicated by “!”. For example, the factorial of 5 is 5x4x3x2x1, which is equal to 120. Therefore, 120 is the factorial of 5!. The understanding of factorials depends heavily on the understanding of algebra, geometry, probability, statistics, number theory, graph theory, etc.

Factorial of 100

For the factorial of 100 we need to understand that 100 consists of more than 10 whole numbers. Having such huge numbers means that it is unlikely to follow each step and calculate the factorial of 100.

Therefore the factorial of 100 can be represented by:

n! = n*(n-1) *(n-2) *(n-3) ….3*2*1

Here n is a natural number that is more than or equal to 1, therefore, by understanding the above formula we can say that if n is equal to 0 then n! would be 1.

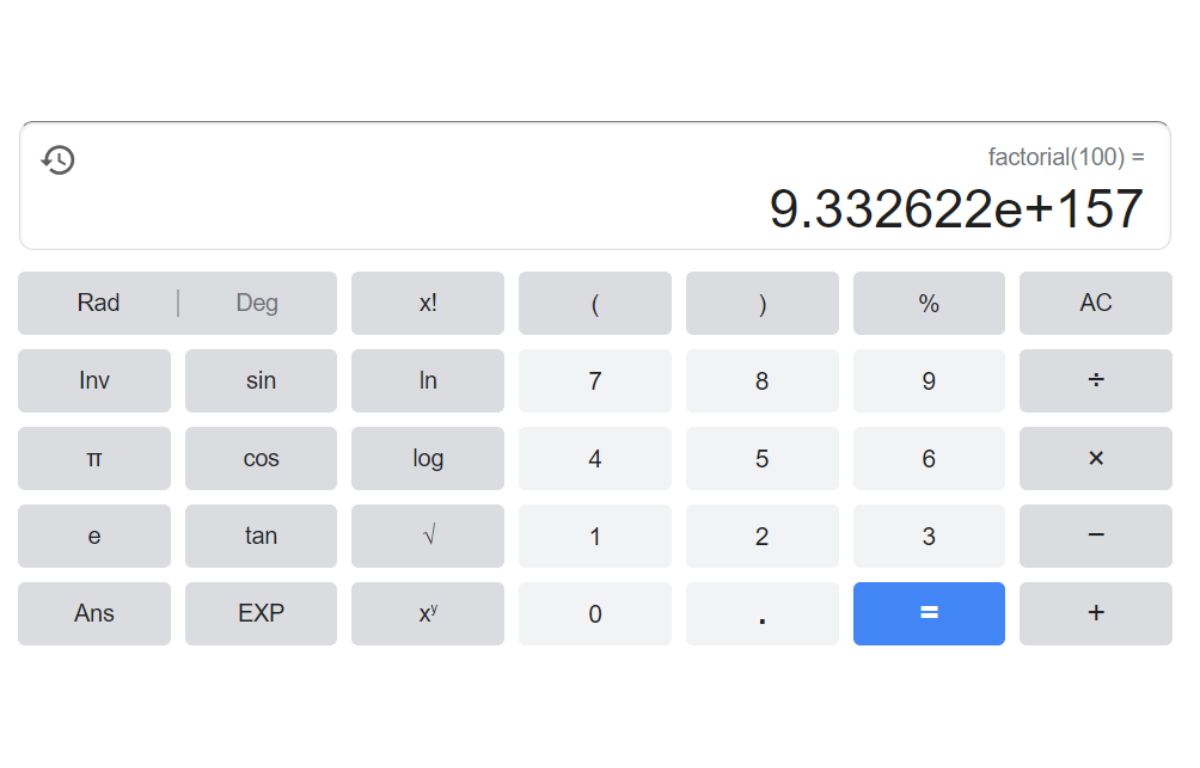
So if we use the formula to calculate the factorial of 100, it can be said that the factorial of 100 would be equal to 9.332621544 E + 157.

Finally, we can say that:

100! = 100x99x98………………..3x2x1 = 9.332621544 E + 157. (What is the Factorial of 100?)

Answer:

100! = 9.332621544 E + 157

What is Factorial?

The factorial of a whole number is a function that multiples the number by every natural number below it. In mathematics, factorials are observed commonly in the process of permutations and combinations. To understand the meaning of factorial check the representation below:

“n!” or “nfactorial” means:

n! = 1 · 2 · 3 · … · n.

The product of first n integers is n(n-1)(n-2)……(2)(1)

Formula of Factorial

To find a factorial of an integer one can either simply use the n (n – 1) (n – 2) ….1 method or can multiply the factorial value of the previous integer with the integer n! = n × (n – 1)!. The table below contains the representation and use of both ways to find the factorial of an integer.

Formula of factorial
n Factorial	n (n – 1) (n – 2) ….1	Result	n! = n × (n – 1)!	Result
1 Factorial	1	1	1	1
2 Factorial	2×1	2	2×1!	2
3 Factorial	3x2x1	6	3×2!	6
4 Factorial	4x3x2x1	24	4×3!	24
5 Factorial	5x4x3x2x1	120	5×4!	120
6 Factorial	6x5x4x3x2x1	720	6×5!	720
7 Factorial	7x6x5x4x3x2x1	5,040	7×6!	5,040
8 Factorial	8x7x6x5x4x3x2x1	40,320	8×7!	40,320
9 Factorial	9x8x7x6x5x4x3x2x1	3,62,880	9×8!	3,62,880
10 Factorial	10x9x8x7x6x5x4x3x2x1	36,28,800	10×9!	36,28,800

What is the Factorial of 100 in Hindi?

100 के फैक्टोरियल के लिए हमें यह समझने की आवश्यकता है कि 100 में 10 से अधिक पूर्ण संख्याएँ होती हैं। इतनी बड़ी संख्या होने का मतलब है कि प्रत्येक चरण का पालन करना और 100 के फैक्टोरियल की गणना करना संभव नहीं है।

इसलिए 100 के फैक्टोरियल को इस प्रकार दर्शाया जा सकता है:

एन! = n*(n-1) *(n-2) *(n-3) ….3*2*1

100! = 100x99x98………………..3x2x1 = 9.332621544 E + 157.

Answer:

100! = 9.332621544 E + 157