Mensuration is a branch of mathematics that deals with geometric figures and their measurement. It deals the parameters like shape, length, volume, area, surface area etc. Mensuration is all about the measurement of the geometrical figures that come under the category of 2D and 3D shapes.
Mensuration Formulas
With the help of the mensuration formulas, you will be able to know and calculate the areas, perimeter, volume, total surface area, curved surface area, length, etc of different geometrical figures. Before moving on to the mensuration formulas, let us first understand the difference between 2D and 3D figures. This article is not just important for school-going students but also for those candidates who are preparing for various competitive exams where mensuration holds a huge weightage. If you are an aspirant of SSC, Bank Exams, or other government exams, you might know that approximately 2-3 questions are asked in the Quantitative Aptitude of SSC CGL, SSC CHSL, SSC MTS, SSC CPO, Delhi Police Constable, Bank Exams paper on mensuration topics. These Mensuration formulas are also important for Class 8, 9 10 students, so stay tuned and allow us to help you master your exams.
Now, you may be clear about 2-D shapes and 3-D shapes, but still, for your better understanding, we will bifurcate the mensuration formula tables for both shapes below. Check out the Mensuration Formulas for 2-D and 3-D shapes below.
Mensuration Formulas for 2-D Figures
The area of 2-D figures is always calculated in square units and the perimeter is always calculated in units. below is the complete list of areas and perimeters of different 2-D figures such as square, triangle (scalene, isosceles, equilateral, right), trapezium, parallelogram, rhombus, circle, etc. Have a look at these mensuration formulas, understand them and learn them by heart.
| Mensuration Formulas for 2-Dimensional Figures | ||
| Shape | Area | Perimeter |
| Circle | πr² | 2 π r |
| Square | (side)² | 4 × side |
| Rectangle | length × breadth | 2 (length + breadth) |
| Scalene Triangle | √[s(s−a)(s−b)(s−c), Where, s = (a+b+c)/2 | a+b+c (sum of sides) |
| Isosceles Triangle | ½ × base × height | 2a + b (sum of sides) |
| Equilateral Triangle | (√3/4) × (side)² | 3 × side |
| Right Angled Triangle | ½ × base × hypotenuse | A + B + hypotenuse, where the hypotenuse is √A²+B² |
| Parallelogram | base × height | 2(l+b) |
| Rhombus | ½ × diagonal1 × diagonal2 | 4 × side |
| Trapezium | ½ h(sum of parallel sides) | a+b+c+d (sum of all sides) |
Mensuration Formulas for 3-D Figures
Under 3-D Figures, we can calculate the total surface area which is equal to curved surface area+ area of top and bottom. Curved surface area is also known as lateral surface area, and is measured in square units. Total surface area is also measured in square units whereas volume is measured in cubic units. So, find out the mensuration formulas for 3-D figures such as cone, cylinder, cube, cuboid, sphere, etc.
| Mensuration Formulas for 3-Dimensional Figures | |||
|---|---|---|---|
| Shape | Area | Curved Surface Area (CSA)/ Lateral Surface Area (LSA) | Total Surface Area (TSA) |
| Cone | (1/3) π r² h | π r l | πr (r + l) |
| Cube | (side)³ | 4 (side)² | 6 (side)² |
| Cuboid | length × breadth × height | 2 height (length + breadth) | 2 (lb +bh +hl) |
| Cylinder | π r² h | 2π r h | 2πrh + 2πr² |
| Hemisphere | (2/3) π r³ | 2 π r² | 3 π r² |
| Sphere | 4/3πr³ | 4πr² | 4πr² |
Differences between 2-Dimensional and 3-Dimensional Figures
There are two types of figures in geometry, one is 2-dimensional and 3-dimensional figures. Check out the table below to know and understand the 2-Dimensional and 3-Dimensional figures and the differences between them.
| 2-Dimensional Figures | 3-Dimensional Figures |
| As the name suggests, a 2D shape means that it will have only 2 dimensions which are length and breadth. | Here, a 3D shape means that this figure will have 3 dimensions, which are length, breadth, and height. |
| For 2D shapes, we can calculate 2 things i.e. area and perimeter. | For 3D shapes, we can calculate their volume, total surface area, and curved/lateral surface area. |
| 2D shapes are flat as they do not have depth and also, these cannot be held physically because of the lack of depth. | 3D shapes contain a depth so they can be held physically and are not flat like 2D shapes. |
| Example: Square, Rectangle, Triangle, Circle, etc. | Example: Cone, Cylinder, Sphere, Cube, Prism, Pyramid, etc. |
Mensuration Formulas PDF
For understanding the mensuration formulas for each 2-dimensional and 3-dimensional figures in-depth, download the pdf from the below link and practice for the questions efficiently. You can also download the Mensuration Formulas PDF from the links given below.
Mensuration Formulas PDF 1- Click to Download
Mensuration Formulas PDF 1- Click to Download
Mensuration Formulas Examples
Mensuration maths formulas for all 2-D and 3-D figures are discussed below in detail.
1. Cube Formula
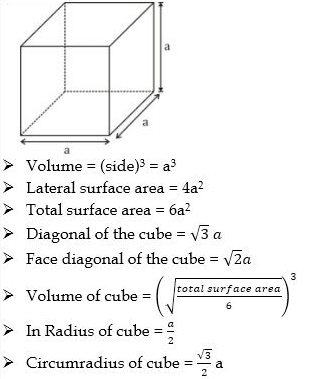
2. Cuboid Formula

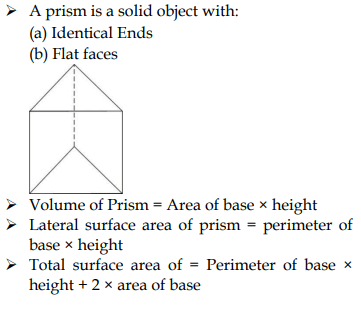
3. Prism Formula
4. Sphere Formula

5. Hemisphere Formula
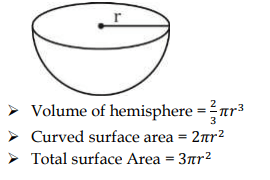
6. Pyramids Formula

7. Right Circular Cone Formula

8. Right Circular Cylinder Formula

9. Equilateral Triangle Formula
Important Terms Related to Mensuration Formula
Before understanding the mensuration formulas, we need to understand certain terms. These are
● Perimeter: This is measured in units such as m, cm, etc and it is the measure of or sum of the continuous length of the boundary of a figure.
● Area: This is measured in square units such as m², cm², etc and it is the surface enclosed in a figure.
● Volume: This is measured in cubic units such as m³, cm³, etc, and is nothing but the space occupied by an object.
● Curved/Lateral Surface area: This is measured in square units such as m², cm², etc and it is the area of the curved surface in a figure.
● Total Surface area: This is measured in square units such as m², cm², etc and it is the area of the total surface in a figure including the top and bottom portions.
Mensuration Questions with Solutions
Q1. Find the area of a rhombus whose diagonals are of lengths 9 cm and 7.2 cm.
Solution: Now, d1=9 cm, d2=7.2 cm where d1 and d2 are the lengths of diagonals of a rhombus.
Area of rhombus formula is ½ (d1xd2)
Therefore, area of the given rhombus = ½ x 9 x 7.2 cm² = 32.4 cm²
Note: Here, the value of π is either considered as 22/7 or 3.14, r means radius, and h means height.
Q2. A rectangular paper of a width of 10 cm is rolled along its width and a cylinder of a radius of 18 cm is formed. Find the volume of the cylinder. (Take π=22/7)
Solution: A cylinder is formed by rolling a rectangle of 10 cm about its width. The radius of the cylinder is 18 cm and the width of the paper becomes the height.
Height of the cylinder, h = 10 cm and Radius of the cylinder, r = 18 cm
Now, volume of the cylinder, V = πr²h = (22/7) x (18)² x 10
= 10,183 cm³
Hence, the volume of the cylinder is 10183 cm³.
Q3. A circle has a radius of 21 cm. Find its circumference and area. (Use π = 22/7)
Solution: We know, Circumference of circle = 2πr = 2 x (22/7) x 21 = 2 x 22 x 3 = 132 cm
Area of circle = πr² = (22/7) x (21)² = 22/7 x 21 x 21 = 22 x 3 x 21
Area of circle with radius, 21cm = 1386 cm²
Q4. The length, width, height of a cuboidal box are 30 cm, 25 cm and 20 cm, respectively. Find its area.
Solution: Here, l- 30 cm, b= 25 cm, and h= 20 cm
Total surface area = 2 (lb +bh +hl)
= 2 (30 × 25 + 25 × 20 + 20 × 35)
TSA = 2( 750 + 500 + 700) = 3900 cm²
Q5. A rectangular piece of paper 11 cm × 4 cm is folded without overlapping to make a cylinder of the height of 4 cm. Find the volume of the cylinder.
Solution: The length of the paper will be the perimeter of the base of the cylinder and the width will be its height.
Circumference of base of cylinder = 2πr = 11 cm
2 x 22/7 x r = 11 cm
r = 7/4 cm
Volume of cylinder = πr²h = (22/7) x (7/4)² x 4 = 38.5 cm³
Q6. The tangents drawn at points A and B of a circle with Centre O, meet at P. If ∠AOB = 120° and AP= 6cm, then what is the area of triangle (in cm²) APB?
Solution:
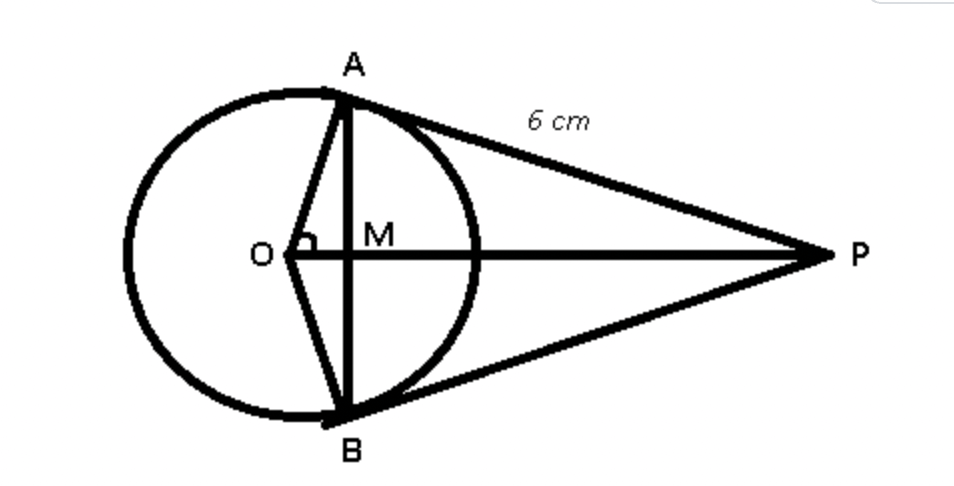
Given ∠AOB = 120° and AP= 6cm and ∠OAP = 90°
∠AOP= ½∠AOB = 120/2 = 60°
In △AOP, >tan (∠AOP) = AP/OA
=> tan 60° = 6/OA
=> √3 = 6/OA
=> OA = 6/√3 = 2√3 cm
Thus, area of △AOP = ½ x (OA) x (AP)
=> ½ x (2√3) x (6) = 6√3 cm² ……………….. (i)
Now, in △AOM
=> sin(∠AOM) = AM/OA
=> sin 60° = AM/2√3
=> √3/2 = AM/2√3
=> AM = 3 cm
Similarly OM= √3 cm
Thus, area of △AOM = ½ x (OM) x (AM)
=> ½ x (√3) x (3) = 1.5√3 cm² ……………….. (ii)
Now, ar(△AMP) = ar(△AOP) - ar(△AOM)
=> 6√3 -1.5√3 = 4.5 √3 cm²
∴ ar(△APB) = 2ar(△AMP)
= 2 x 4.5√3 = 9√3 cm²
Q7. The total surface area of a hemisphere is 166.32 cm², find its curved surface area?
Solution: Let radio of hemisphere = r cm
Tital surface area of hemisphere = 3 π r² = 166.32 ……………….. (i)
Multiplying equation (i) by ⅔
=> ⅔ x 3 π r² = ⅔ x 166.32
=> Curved surface area of hemisphere = 2 π r² = 2 x 55.44 = 110.88 cm²
Q8. If G is the centroid and AD, BE, and CF are three medians of the triangle with 72 cm², then the area of triangle BDG is:
Solution: The area of the triangle formed by any two vertices and centroid is ⅓) times the area of △ABC.
Also, the median divides the triangle into two equal areas.
So, the area of △BDG = 1/6 times of △ABC
=> 1/6 x 72
=> 12
Q9. The perimeters of two similar triangles ABC and PQR are 156 cm and 46.8 cm respectively. If BC= 19.5 cm and QR= x cm, then the value of x is?
Solution: (△ABC) Perimeter/ (△PQR) Perimeter) = BC/QR
=> 15.6/46.8 = 19.5/x
=> x = 46.8 x 19.5 / 156
=> 5.85 cm
Q10. A solid metallic sphere of radius 10 cm is melted and recast into spheres of radius 2 cm each. How many such spheres can be made?
Solution: As, V = 4/3 π r³
Volume of big sphere = n x volume of small sphere
=> 4/3 π (10)³ = n x 4/3 π (2)³
=> n = 125
Conclusion
Mensuration is an interesting yet difficult topic to cover because it is vast and needs practicality. Also, there are large amounts of formulas that some students find difficult to retain. Well, this can be made easy if you regularly practice a few questions on the topic and revise all the formulas on a daily basis. We hope that you find this article on Mensuration Formulas beneficial and informative. Stay connected with us for more such articles.
