Ratio and Proportion Formula: The topics of Ratio and Proportion are discussed based on the fractional numbers. If a fractional number is expressed in the form of a : b then it is called a ratio while a proportion refers to that two ratios are the same. Here a and b are considered two integers. The ratio and proportion are the foundation topics of Mathematics to understand several other mathematical concepts. In day-to-day life, we commonly apply the concept of ratio and proportion like a business deal in money, comparing heights and weights with that of others, adding ingredients while cooking dishes in the kitchen, etc. In this article, we explain completely the topics of Ratio and Proportion, the Definition of Ratio and Proportion, Ratio and proportion Formula, the Difference between Ration and Formula, and solved problems of ratio and proportion.
Ratio and Proportion
Many times, students get puzzled by the concept of ratio and proportion. A comparative analysis of two parameters with the help of a division operator is called a Ratio. The similarity of two different ratios in terms of value is called a Proportion. A ratio can be expressed in a different manner such as x : y or x / y. It is to be read as x is to y. However, a proportion is a mathematical equation that states that two ratios are equal. A proportion is expressed as x : y : : p : q. It is to be read as x is to y as same as p is to q. Here denominators y & q are not equivalent to 0 in terms of value.
Definition of Ratio
A Ratio is defined as the comparison of 2 parameters which is done by using the division operator between the first quantity and the second. When x and y are 2 parameters of the same type and with similar units like y is not equivalent to 0 then the quotient x/y is generally known as the ratio between x and y. Ratios are represented with the help of the colon sign (:). It means that the ratio x/y is unitless and it can be expressed as x : y. In another word, we can say that the ratio is the number that is applied to represent one quantity as in a fractional form of the other quantity. The two quantities in a ratio can be compared only if these quantities have the same unit.
Definition of Proportion
A Proportion is defined as a mathematical expression stating that the 2 given ratios are similar to each other. In simple words, the proportion is the similarity of the two fractional numbers or the ratios. When the 2 sets of given quantities are increased or decreased in a similar ratio, then those ratios are meant to be directly proportional to one another. Proportions are indicated by the sign (: :) and it helps to find out the unknown numbers.
Types of Proportion
There are two types of proportions as follows.
1. Direct Proportion
Direct proportion refers to the direct relationship between the 2 numbers. If one number increases, then the other number also increases, and vice-versa. Hence the direct proportion is expressed as a ∝ b. For example, when the speed of a vehicle is increased, then its traveling distance will be surely more.
2. Inverse Proportion
Inverse proportion refers to the inverse relationship between the 2 numbers where when one number increases, then the other number decreases, and vice-versa. Hence the inverse proportion is expressed as a ∝ 1/b. For example, when we drink more water from a bottle, then the remaining water quantity in that bottle will be lesser.
Ratio and Proportion Formula
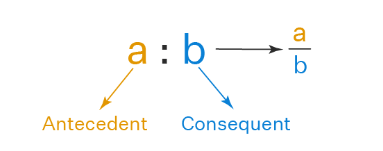
The Ratio Formula is written as x : y ⇒ x/y where
x = Antecedent or The first term
y = Consequent or The second term
For example, Ratio 5 : 4 is also written as 5/4, where 5 is called the antecedent and 7 is called the consequent.
In order to write a proportion in mathematics for the two ratios, a : b and p : q then we express it as a : b :: p : q ⟶ a/b = p/q
- The two numbers namely b and p are called the mean terms.
- The two numbers namely a and q are called the extreme terms.
- In a : b = p : q, the numbers or parameters of a and b should be of the same type with similar units, while p and q may be the separate ratios of parameters of the same type with similar units. For example, 6 meter : 17 meter = 35 kg : 22 kg
- In the concept of proportion, the product of the mean terms is equivalent to the product of the extreme terms. Hence we get b × p = a × q.
- For example, In the proportion of two ratios of 4 : 8 :: 5 : 10, we apply the formula of The Product of Mean Terms = The Product of Extreme Terms
We get, 8 × 5 = 4 × 10 = 40
- The proportion formula can be written in the form of a/b = c/d or a : b : : c : d.
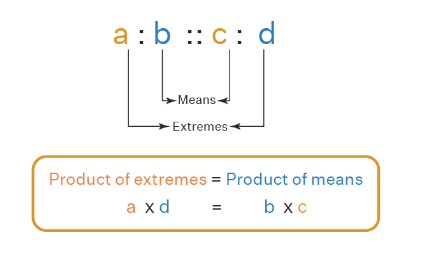
Difference Between Ratio and Proportion
The ratio and proportion are considered the single topic of mathematics with similar concepts being used in these. Sometimes, students get puzzled by these terms ratio and proportion. Here is the comparison between ratio and proportion for a clear understanding.
| Ratio | Proportion |
| It is employed in the comparison of different quantities having the same units. | It is employed in expressing a relationship between two ratios and both ratios can have different units. |
| A colon (:), slash (/) symbols are used to express a ratio. | The double colon (::) symbol is used to express a proportion. |
| It is described as an expression. | It is described as an equation. |
Key Notes on Ratio and Proportion
- Any quantities/ parameters having similar units can be compared by using the concept of ratio.
- Always 2 ratios are known to be in a proportion relation only when they are the same.
- For checking out the equality of two ratios and their status in proportion, you can also apply the method of cross-multiplication.
- When you multiply and divide each number of a ratio by a similar number, then the ratio always gives similar results.
- In the case of any 3 quantities, when the ratio between the 1st and the 2nd quantity is equivalent to the ratio between the 2nd and the 3rd quantity, then this equation is considered the continued proportion.
- Similarly, for any 4 quantities in a continued proportion equation, the ratio between the 1st and the 2nd quantity is equivalent to the ratio between the 3rd and the 4th quantity.
Ratio and Proportion Solved Examples
Question 1: There are 49 students available in the 5th class. The number of students who want to study Social Science and the number of students who want to study Science is expressed in the ratio 5:2. Calculate the number of students who want to study Social Science and those who want to study Science.
Solution: Given that, the total number of students in the 5th class = 49
Let the number of students who want to study Social Science = 5x and
the number of students who want to study Science = 2x
As per the question, we can say that 5x + 2x = 49 ⇒ 7x = 49 ⇒ x = 7
After putting the value of x = 7,
we get the numbers of students who want to study Social Science = 5x = 5 × 7 = 35 and the number of students who want to study Science = 2x = 2 × 7 = 14
Hence 35 students of class 5th want to study Social Science and 14 students want to study Science.
Question 2: If there are two ratios as given 7:8 and 4:3 then find out whether these ratios are in proportion or not.
Solution: The given two ratios are 7:8 and 4:3
By using the division operator of mathematics, we get
7:8= ⅞= 0.875 and 4:3 = 4/3 = 1.33
Both ratios are not equal in value. So 7:8 and 4:3 are not in proportion.
Question 3: Imagine person P and person Q started a shop and made a decision to divide the profit between them in a ratio of 6:5. The total profit from that shop is Rs. 5,000 by the end of the financial year 2020. What will be the individual profit share for both P and Q?
Solution: The total profit earned from the shop is to be divided between P and Q in a ratio of 6:5.
Hence we can calculate the individual profit of both persons by
P= 5,000 x (6/11) = 2727.27
B = 5,000 x (5/11) = 2272.72
Hence the individual profit for both person P and Q will be 2727.27 and 2272.72.
Question 4: If Sahil travels a distance of 15 km in 3 hours. What distance will he travel in the time of 7 hours?
Solution: Let us consider the traveling distance to be z in the time of 7 hours. With time, the traveling distance is also increased.
So, 3 : 7 = 15 : z
z = (15 x 7) / 3
= 35 km
Thus Sahil will travel a distance of 35 km in 7 hours.
Question 5: Calculate the numbers whose sum is 99 and they are written in the ratio of 5:4.
Solution: Let us consider the numbers to be 5x and 4x, respectively.
As per the question, the sum of the considered two numbers is 40.
Now, 5x + 4x = 99
9x = 99
x = 11
Hence the two numbers will be
5x = 5 x 11 = 55
4x = 4 x 11 = 44
55 and 44 are the two numbers that satisfy the given statement of the question.
