Types of Triangles: In the study of geometry, a triangle is defined as a polygon having three angles subtended by three sides. The addition of all interior angles made by the sides of a triangle is always 180 degrees. It is known as the angle sum property of a triangular geometry. On the basis of angles and sides of the triangles, Triangles are mainly classified into 6 types. All different triangles consist of different properties. In this article, you will know more about the different types of triangles with a detailed explanation of their properties.
What are the Different Types of Triangles?
The triangle is one of the common geometrical shapes which is seen in our surroundings from sandwiches to traffic signs. It is rigid and stable in shape so it is generally used in construction. It can be mainly classified into two bases as one type is based on the sides while another type is based on the interior angles of triangles.
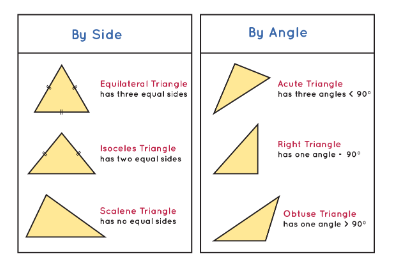
Types of Triangles Based on Sides
The different features of the sides of a triangle make the classification of triangles. The different types of triangles based on sides are explained below.
| Types of Triangles Based on Sides |
| 1. Equilateral Triangle |
| 2. Isosceles Triangle |
| 3. Scalene Triangle |
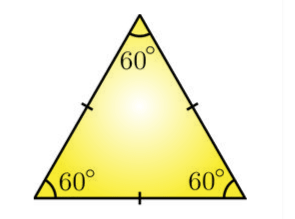
1. Equilateral Triangle
If a triangle has an equal length on all its three sides then it is called an equilateral triangle. In this triangle, the value of each interior angle is 60 degrees. As the angles of this triangle are equal in value so it is also called the equiangular triangle. The figure of an equilateral triangle is shown below.
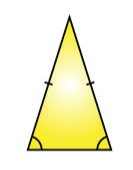
2. Isosceles Triangle
If a triangle has two equal sides out of its three sides then it is called an isosceles triangle. In this triangle, the opposite angles subtended by the same sides are the same as each other. In simple words, an isosceles triangle has 2 similar sides and 2 similar angles. The equilateral and isosceles types of triangles have their reflection symmetry. The figure of an isosceles triangle is shown below.
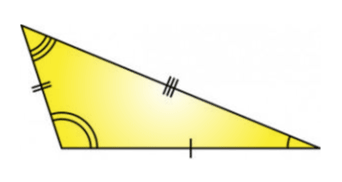
3. Scalene Triangle
If a triangle has different lengths on its three sides then it is called a scalene triangle. In this triangle, there are no equal sides and no equal interior angles. The figure of a scalene triangle is shown below.
Types of Triangles Based on Angles
The different features of the interior angles of a triangle make the classification of triangles. The different types of triangles based on angles are explained below.
| Types of Triangles Based on Angles |
| 1. Acute-angled Triangle |
| 2. Obtuse-angled Triangle |
| 3. Right-angled Triangle |
1. Acute-angled Triangle
If a triangle has all acute interior angles means having less than 90-degree angles then it is called an acute-angled triangle. The figure of an acute-angled triangle is shown below.
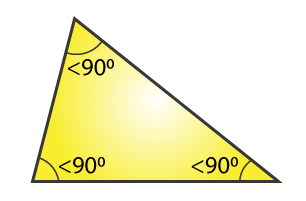
2. Obtuse-angled Triangle
If a triangle has one obtuse angle means having greater than 90-degree angles out of its three interior angles then it is called an obtuse-angled triangle. The figure of an obtuse-angled triangle is shown below.
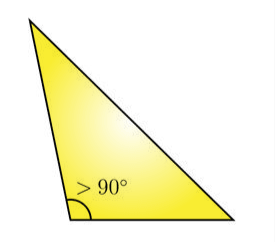
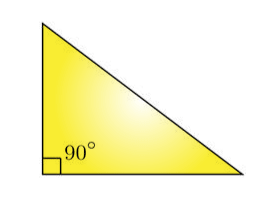
3. Right-angled Triangle
If a triangle has one right angle means having a 90-degree angle out of its three interior angles then it is called a right triangle. In this triangle, the side present opposite the 90-degree angle is the longest side while the other two sides are relatively smaller sides of that triangle. The longest side of this triangle is known as the hypotenuse. The figure of a right triangle is shown below.
Many a time, you have heard the combined names of triangles like the right isosceles triangle which means a triangle having two equal sides and two equal angles with a 90-degree angle.
