Newton’s Second Law: Newton’s Second Law of Motion, formulated by Sir Isaac Newton, states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. The equation F = ma represents this law in math. In this equation, F stands for the force acting on the object, m is the object’s mass, and a is the object’s acceleration. This fundamental principle underpins our understanding of how objects respond to external forces, guiding everything from everyday motion to space exploration, and offering universal insights into the behavior of matter in the universe.
What is Newton’s Second Law of Motion?
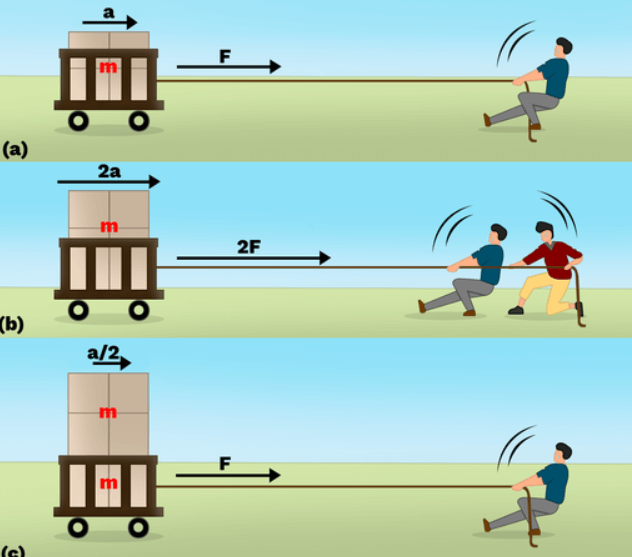
Newton’s second law of motion states that how fast an object speeds up (acceleration) depends on two things: the force applied to it and its mass (weight). If more force is used, the object will accelerate faster. However, if the object is heavier, it will accelerate more slowly. This means acceleration increases with more force but decreases with more mass. So, the force makes it speed up, and its weight affects how much it speeds up. So it can be written as-
a = F/ m (This equation shows that acceleration is inversely proportional to the mass of the body)
F = ma( This equation shows that acceleration is directly proportional to the net force acting on the body)
Newton’s Second Law Formula
Newton’s Second Law of Motion, expressed as the mathematical formula F = ma, is a fundamental principle in classical mechanics. This formula establishes a direct relationship between force (F), mass (m), and acceleration (a) for an object subjected to a net force. As a cornerstone of physics, Newton’s Second Law formula plays a pivotal role in explaining object motion under external forces, enabling applications in diverse scientific and engineering fields, from comprehending planetary motion to designing vehicles and structures.
Mathematical Formula of Second Law of Motion
Suppose a body of mass(m) is moving in a straight line with its initial velocity(u). It is uniformly accelerated to velocity(v) in time(t) by the application of a constant force(F) throughout the time(t).
The initial and final momentum of the body becomes,
p1 = mu
p2 = mv
Therefore, Change in Momentum ∝ p2 – p1
∝ mv – mu
∝ m × (v – u)
Velocity is equal to displacement upon the time taken
Then, the rate of change of momentum ∝ m×( v − u )/t
The applied force will be, F ∝ m×(v- u)/t
F = k m(v-u)/t
F = k ma
Here, a = (v-u)/t is the acceleration.
F = Net force applied
m = mass of the body
k = proportionality constant
| Formulation of Force for Changing and Constant Mass | |
| For changing mass | F = m1v1-m0v0/t1-t0 |
| For constant mass | F = m(v1 – v0/t1-t0) |
SI Unit of Force
The SI units of mass and acceleration are kg and m/s² respectively.
1 unit of force = k × (1 kg) × (1 m/s²).
F = ma
The SI unit of force is kg m/s² or newton, which has the symbol N.
Application of Second Law of Motion
The second law of motion, Newton’s second law of motion explains that the force exerted on an object is directly proportional to both the mass of the object and the acceleration it experiences. This relationship is expressed mathematically as F = ma, where “F” stands for force, “m” represents mass, and “a” denotes acceleration. These are just a few examples of how Newton’s second law of motion is applied in real-world situations. Here are some key applications:
Pushing of Car and Truck
When pushing a car or truck, more force is needed for a heavier vehicle (truck) compared to a lighter vehicle (car). The acceleration of each vehicle depends on its mass and the applied force.
Pushing of Shopping Cart
The force applied to a shopping cart causes it to accelerate. A loaded cart requires more force to push than an empty one because its mass increases, demonstrating that force and acceleration are proportional to mass.
Kicking a Ball
When kicking a ball, the applied force determines its acceleration. A stronger kick causes the ball to accelerate faster, while the mass of the ball influences how much it accelerates, showcasing the second law in action.
Two People Walking
When two people walk, the person applying more force on the ground accelerates faster. Their different masses and forces impact their acceleration, showing the relationship between mass, force, and movement according to Newton’s second law.
Rocket Launch
During a rocket launch, immense force is exerted by the engine to overcome the rocket’s mass. As the force increases, so does the rocket’s acceleration, demonstrating the relationship between mass, force, and acceleration.
Car Crash
In a car crash, the force applied to the car and its occupants causes rapid deceleration. A heavier car will require more force to stop, and the effects of the crash depend on the vehicle’s mass and speed.
Exercise based on Newton’s Second Law
Q1. A truck is moving with a velocity of 30m/s and it takes 5s to stop after the brakes are applied. Calculate the force exerted by the brakes on the truck if its mass along with the passengers is 1500 kg.
Solution: According to the question,
The initial velocity of the motorcar, u = 30m/s
The final velocity of the motorcar, v = 0 m s-1
On substituting the values, we get F = 1500 kg × (0 – 30) m s-1/5 s
= – 9000 kg m/s² or – 9000 N.
The negative sign tells us that the force exerted by the brakes is opposite to the direction of motion of the motorcar.
Q2.If there is a block of mass 4kg, and a force of 30 N is acting on it in the positive x-direction, and a force of 50 N in the negative x-direction, then what would be its acceleration?
Solution: Net Force = 30N – 50N
Net Force = -20N
Acceleration = -20/4 = -5m/s²
The negative acceleration indicates that the block is slowing and its acceleration vector is moving in an opposite direction directed opposite to the direction of motion.
| Related Links | |
| Newton’s Laws of Motion | Newton’s First Law |
| Kepler’s law | Ohm’s Law |



 Ohm's Law: Definition, Formula, Limitati...
Ohm's Law: Definition, Formula, Limitati...
 Newton's First Law of Motion: Definition...
Newton's First Law of Motion: Definition...
 Kepler's Laws of Planetary Motion: First...
Kepler's Laws of Planetary Motion: First...













