In astronomy, Kepler’s laws of planetary motion were published by Johannes Kepler between 1609 and 1619 describing the orbits of planets around the Sun. His laws were the modified version of the heliocentric theory of Nicolaus Copernicus. Kepler’s laws of planetary motion topic is included in the CBSE class 11 Physics syllabus under the Gravitational chapter. In this article, we will delve into the intriguing world of Kepler’s Laws, exploring their significance, formulation, and applications, while providing valuable insights for both astronomy enthusiasts and curious minds.
Kepler’s Law of Planetary Motion
Kepler gave three laws to study planetary motion. Kepler’s laws of planetary motion are three scientific laws describing the motion of planets around the sun. Three of Kepler’s laws are:
- Kepler’s First Law (The Law of Ellipses): All planets orbit the Sun in an elliptical orbit, the Sun being the center.
- Kepler’s Second Law (The Law of Equal Areas): A line segment joining a planet and the Sun gives out equal areas during equal intervals of time.
- Kepler’s Third Law (The Law of Harmonies): The square of a planet’s orbital period is directly proportional to the cube of the length of the semi-major axis of its orbit.
Kepler’s First Law of Planetary Motion
The first law of planetary motion is also called as Law of Orbit. Kepler’s first law of motion says, “All the planets revolve around the sun in elliptical orbits having the sun at one of the focus points”. This means that the paths traced by planets deviate from perfect circles and can vary in eccentricity. In simpler terms, planets do not move in perfect circles, but rather follow elliptical paths with the Sun at one of the focal points.
The point at which the planet is close to the sun is called a Perihelion, and the point at which the planet is farthest from the sun is called Aphelion.
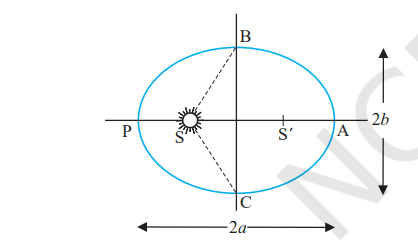
(An ellipse traced out by a planet around the sun. The closest point is P and the farthest point is A, P is called the perihelion and A the aphelion. The semimajor axis is half the distance AP.)
Understanding Kepler’s first law allows astronomers to determine the eccentricity and shape of planetary orbits accurately. It dispelled the ancient belief that celestial bodies move in perfect circles and paved the way for a more accurate description of the solar system’s structure.
Kepler’s Second Law of Planetary Motion
The second law of Kepler’s law of Planetary Motion is also called as “Law of Equal Areas”. Kepler’s second law says, “The radius vector that is drawn from the sun to the planet gives out equal areas in equal intervals of time”. In other words, a planet moves faster when it is closer to the Sun and slower when it is farther away. This law highlights the fact that planets do not move at a constant speed throughout their orbits.
As the orbit is not circular, so the planet’s kinetic energy is not constant in its path. Its kinetic energy is more near the Perihelion whereas the kinetic energy is near the aphelion. This implies that at perihelion, speed is more and at Aphelion, speed is less.
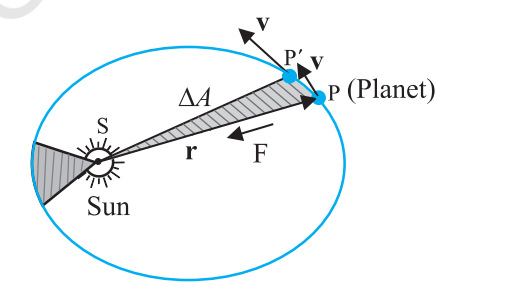
(The planet P moves around the sun in an elliptical orbit. The shaded area is the area ∆A swept out in a small interval of time ∆t.)
Kepler’s Third Law of Planetary Motion
The third law of Kepler’s is also known as the Law of Harmonies and the Law of Periods. Kepler’s Third Law establishes a mathematical relationship between a planet’s orbital period and its average distance from the Sun. According to this law, “The square of the time period of revolution of a planet (T) is proportional to the cube of the semi-major axis of the ellipse traced out by the planet (a).”
T² ∝ a³
Where,
T is the time period of the planet
a is the semimajor axis
Kepler’s Third Law plays a crucial role in determining the relative sizes and distances of planets within our solar system. It has also facilitated the discovery of exoplanets, planets orbiting stars beyond our solar system, by analyzing the variations in light as these exoplanets transit in front of their host stars.
Derivation of Kepler’s Third Law
Assume, the mass of the planet is (m) and revolves around the Sun of mass (M) with velocity(V)
So, the force of gravitation between the Sun and the planet is-
F = GmM/r²
As it is moving in an elliptical orbit, the centripetal force also applies here-
Fc = mv²/r²
Therefore, F = Fc
⇒GmM/r² = mv²/r²
⇒ GM = v² ……………….. (1)
As we know, v = circumference time = 2πrt ………………..(2)
Comparing the equations, we get
⇒ GMr = 4π²r²T²
T² = 4π2r3)GM
⇒ T² ∝ r³ Hence Proved
History of Kepler’s Law of Planetary Motion
The foremost model for planetary motions proposed by Ptolemy was a ‘geocentric’ model in which all celestial objects including stars, the sun and the planets, all revolved around the earth. The only possible move that was thought to be possible for celestial objects was moving in a circle. Later on, similar other theories were also advanced by Indian astronomers. However, a more elegant model in which the Sun was the centre around which the planets revolved was already mentioned by Aryabhatta in his treatise(that was heliocentric theory).
A thousand years later, a monk named Nicolas Copernicus proposed a defined model in which the planets move in circles around the sun in a fixed path. But his theory was discredited by many. A nobleman called Tycho Brahe belonging to Denmark spent his entire lifetime recording observations of the planets with the naked eye. His compiled data was, later on, analysed by his assistant Johannes Kepler. He proposed three elegant laws that now is named Kepler’s laws.
Application of Kepler’s Law
Kepler’s laws describe the orbits of planets around the sun or stars around a galaxy in classical mechanics. They have been used to predict the orbits of many objects such as asteroids and comets , and were pivotal in the discovery of dark matter in the Milky Way.
- Kepler’s law applies to any satellite, whether natural or man-made satellite.
| Related Links | |
| Newton’s Laws of Motion | Newton’s First Law |
| Ohm’s law | |



 Top 5 IPMAT Coaching in Noida – Your G...
Top 5 IPMAT Coaching in Noida – Your G...
 Top 5 IPMAT Coaching in Delhi NCR (Updat...
Top 5 IPMAT Coaching in Delhi NCR (Updat...
 Top 5 IPMAT Coaching in Gurugram for Com...
Top 5 IPMAT Coaching in Gurugram for Com...













