Circle in Maths, Formula, Definition, Properties, Objects

What is Circle?

The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane is called a Circle. To describe in Mathematics or Geometry, the circle is a special type of ellipse in which eccentricity is zero and two foci are coincident. It is also defined as the locus of all points that are drawn equidistant from the centre point. The Circle is a two-dimensional figure which divides a plane into interior and exterior regions. Circle has got its own area ns perimeter, measured in terms of its radius.

In this article, we are covering all the details of a Circle like Definition, Properties, Examples/Objects and all formulas. Let us look through more facts about circles in this article.

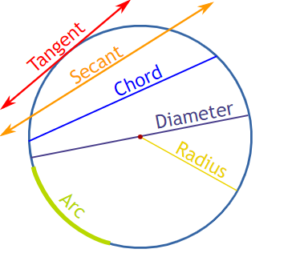
Important Terms related to Circle

Centre (केंद्र): Centre is the point which is equidistant from all the points on the circle.

Radius (त्रिज्या): Radius is the fixed distance from any point on the circle to the centre of the circle.

Chord (जीवा): Chord is the line segment, which is formed by joining any two points on the circle. 

Diameter (व्यास): Diameter is the largest chord that passes through the centre of the circle. It divides the circle into two equal parts

Circumference(परिधि): The Circumference of a circle is the curve length or distance around the circle.

Arc (चाप): It is a portion of the circumference of a circle.

Sector (त्रिज्यखंड): A sector of a circle, is the portion of the area of the circle enclosed by two radii and a common arc.

Segment (वृत्तखण्ड): It is the area of the circle surrounded by a chord and the arcs formed by joining the points on the circle from which the chord is formed.

Tangent(स्पर्शरेखा): It is the line segment that touches the circumference of the circle only at one point. The tangent at any point of the circle is perpendicular to the radius formed from that point of contact on the circle. 

Semi Circle (अर्धवृत्त): It is formed by diameter and the arc connecting endpoints of the diameter. A semicircle is formed when a lining passing through the centre touches the two ends of the circle.

Secant (काटनेवाला): Secant is a straight line that intersects a circle in two points, whereas chord touches the circle at two points.

All formulas of the circle

The following are the important math formulas that are related to a circle. Memorising all these circle formulas helps you score well in your school exams and other competitive exams.

• Radius of Circle = Diameter⁄2
• Area of Circle = πr²  (π=22⁄7  )
• Circumference of Circle = 2πr
• Area of a Semi-circle = r⁄22
• The perimeter of the Semi-circle = πr+2r
• Diameter of a Circle = 2r

Formulas for Sector and Segment of a Circle

Sector (त्रिज्यखंड)

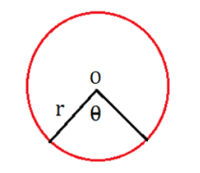
• Area of Sector = θ/360×πr²
• Perimeter of Sector = θ/360×2πr+2r
• Length of the arc of Sector = θ/360×2πr

Segment (वृत्तखण्ड)

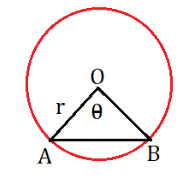
• Area of Segment = Area of the sector – Area of Triangle
•                                 θ/360×πr² – 1⁄2r²Sinθ

• Perimeter of Segment = θ/360×2πr+2rSin(θ/2)

Circumcircle:  Circumcircle is a circle that passes through each vertex of the triangle, and its centre is known as a circumcenter.

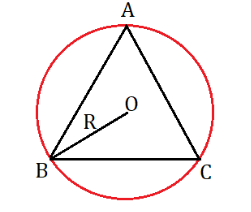
Here ‘R’ is called the circumradius of the circle.

Incircle

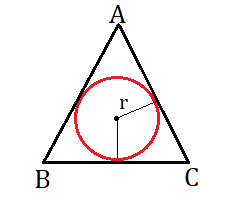
It is the largest circle in the triangle that touches each side of the triangle and its centre is known as the incenter. All sides of the triangle act as the tangent to the circle. Here ‘r’ is called the inradius of the circle.

An important result for circumcircle and incircle for some triangles

Equilateral Triangle:  Triangle whose all sides are equal

• Circumradius = side⁄√3 cm.
• Inradius = side⁄2√3 cm.
• Circumradius + Inradius of equilateral triangle = Height of triangle
• Circumradius of equilateral triangle = 2× Inradius of an equilateral triangle

 Right angle Triangle: Triangle whose one angle is 90°.

• Circumradius = Hypotenuse⁄2
• Inradius = base+perpendicular-Hypotenuse⁄2

Properties of Circle

Some of the important basic properties of circles are as follows:

• The circle’s outer line is equidistant from the center.
• The diameter of the circle divides the circle into two equal halves.
• Circles with equal radii are congruent to each other.
• Two circles that differ in their size and radii are said to be similar.
• The diameter of the circle is double the radius, which is the largest chord.
• The area of a circle is the space enclosed by its boundary and it is calculated using the formula Area = π × r², where r is the radius.
• The circumference of a circle is the distance around its boundary and It is calculated using the formula: Circumference = 2 × π × Radius.

Circle Shaped Objects

In the real world, there are so many objects which are circular in shape. Circle-shaped objects are geometric shapes that have circular or round outlines. Some of the Circle-shaped objects are as below:

• Coins: Coins are often circular and have varying designs and values based on their country of origin.
• CDs and DVDs: These optical storage media have circular shapes and are used for storing digital data.
• Buttons: Many buttons, whether on clothing or electronic devices, are circular in shape.
• Wheels: The outer edge of a wheel is typically circular. Wheels are used in various applications, from vehicles to machinery.
• Plates: Dinner plates and other round dishes are circle-shaped objects that are commonly used for serving food.
• Frisbees: A frisbee is a flying disc that has a circular shape and is often thrown for recreational play.
• Clocks: The face of a clock is circular, and the hands move around the center to indicate the time.
• Pizzas: Pizzas are often circular in shape, with various toppings and a circular crust.
• Earrings: These types of earrings are typically circular and worn in pierced ears.
• Tires: The outer portion of a tire is circular and makes contact with the road when a vehicle is in motion.

Sharing is caring!