Pythagoras theorem, also known as Pythagorean theorem, is one of the most important concepts in Mathematics which is concerned with the right-angled triangle. The theorem is named after the famous Greek philosopher Pythagoras, who first proved this famous theorem and deduced its equation. This theorem explains the relation between the sides of a right-angled triangle. The sides of a right-angled triangle are called Pythagorean triples. Pythagorean formula finds many applications and is one of the most widely used formulas in mathematics.
The three sides of a right-angled triangle are called Base, Hypotenuse, and Perpendicular. The longest side is known as hypotenuse. It is the side opposite to the right angle (900). The other two sides are called the base and perpendicular/height (both can be used interchangeably). Knowing these details, we can now understand the formal statement and terminologies of the Pythagoras theorem. Let us learn about this theorem in detail.
Pythagoras Theorem states
Pythagoras formula is widely used to find the dimension of the unknown angle and side of a triangle. The official Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides (base and perpendicular)”. In other words, the square of the longest side of a right-angled triangle is always equal to the sum of squares of the other two shorter sides. This theorem holds true only in the case of right-angled triangles. Let us understand this concept through an example.
Let us assume a right-angled triangle ABC with right-angled at A. The longest side or hypotenuse will be therefore BC (opposite to A). The other two sides, AB and AC, will be base and perpendicular. So according to the Pythagoras theorem, the square of BC will be equal to the sum of squares of AB and AC.
Pythagoras Theorem Formula
The formula of the Pythagoras theorem explains its statement in the equation form. Let us understand this famous formula through an example.
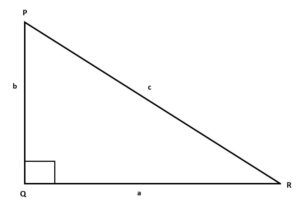
Suppose a right-angled triangle PQR. Let there be three sides a, b, and c.
Where “a” is the base
“b” is the perpendicular
“c” is the hypotenuse
As per the definition of the Pythagoras Theorem, the Pythagoras theorem formula is given by,
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
c2= b2 + a2
As stated above, the Pythagoras theorem defines the relationship between sides of a right-angled triangle. One can easily find the sides and angles (using trigonometry) of a right-angled triangle using the Pythagorean formula. Let us understand the usefulness of this formula through an example.
Pythagoras Theorem Example
Solved Example: Observe the right-angled triangle given below. Find the missing value of Z for this triangle.
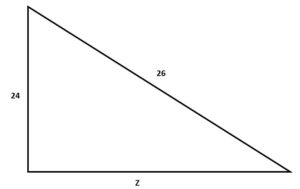
Solution: As the dimension of the side opposite to the right angle is 26 units. So, it is the length of the hypotenuse.
The length of the perpendicular is 24 units.
So, Z here is the base whose length is to be found.
Given, hypotenuse = 26 units
Perpendicular = 24 units
Base= Z
According to the Pythagoras theorem,
Hypotenuse2= perpendicular2 + base2
262= 242 + Z2
676= 576 + Z2
676-576= Z2
Z2= 100
Z= √100
Z= 10 units
Therefore, the value of the base (Z) is 10 units.
This example showed you the importance of the Pythagoras theorem for a right-angled triangle. Using this theorem, you can easily find the missing values in a right-angled triangle.



 Integration Formula for Class 12th, Conc...
Integration Formula for Class 12th, Conc...
 Maths Formulas for Class 10 Chapter wise
Maths Formulas for Class 10 Chapter wise
 What is the Factorial of 100?
What is the Factorial of 100?













