Isosceles Triangle – Properties, Angles, Area, Formula and Types

While eating a Samosa or viewing a pyramid on your device, one geometrical shape would have crossed your mind. You guessed it right, that very shape is a Triangle. Triangles are three-sided polygons having three edges and three vertices. The edges and vertices can be equal or unequal in length. Based on these similarities and dissimilarities, triangles are classified into several types. One of the three major types of triangles on the basis of the length of sides is the Isosceles Triangle.

What is an Isosceles Triangle?

Isosceles Triangles are those triangles whose two sides are equal in length. If any two sides of a triangle have the same measurement, then that triangle is known as the Isosceles triangle. Also, the angles opposite to the equal sides are equal. To sum up, it can be said that Isosceles triangles whose two sides are congruent and the angles opposite to those sides are also congruent.

Example of Isosceles Triangle

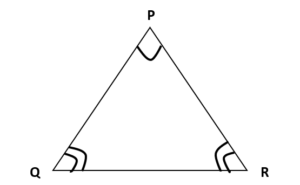
Let us understand this concept by taking an example. Suppose a triangle with three vertices PQR. In triangle PQR, if sides PQ and PR are equal, then the triangle PQR is an Isosceles triangle. The angles opposite to the equal sides are also equal, i.e., ∠P=∠Q. Basically, as per the theorem for the Isosceles triangle, “If the two sides of a triangle are congruent, then the angles opposite to them are also equal and vice versa”.  The triangle has been drawn below.

Properties of Isosceles Triangle

Isosceles triangles show some features that make it unique from other triangles. These features help to identify Isosceles triangles quite easily. The properties of Isosceles triangles are mentioned hereunder:

• An Isosceles triangle consists of two equal sides and two equal angles (angles opposite to the equal sides).
• Two equal sides are called the legs and the angle made by those sides is called the vertex angle or apex angle.
• The unequal side is called the base of the triangle.
• The perpendicular drawn from the apex angle bisects both the apex angle and the base.
• The perpendicular line from the apex angle to the base divides the isosceles triangle into two congruent triangles, thus this perpendicular line is also known as its line of symmetry.

Angles of Isosceles Triangle

As mentioned above, the angles opposite to the equal sides of an isosceles triangle are equal in measurement. The third angle, also known as the apex angle, is unequal. The unequal angle of a right isosceles triangle is always 90°. So, if any one of the angles of an isosceles is known to us, then we can easily deduce the rest of the angles by using the angle sum property of the triangle.

For example, let the measure of the unequal angle of an Isosceles triangle be 80°. Then we can find the rest of the two angles by using the angle sum property. As we know the other two angles will be equal, let them be x. Then according to the angle sum rule,

80° + x + x = 180°

2x = 180° – 80°

2x = 100°

x = 100° / 2

x = 50°

See, how easy it is to find the angles of an Isosceles triangle using the angle sum property.

Area of an Isosceles Triangle

The area of an isosceles triangle refers to the region occupied by it in the 2-D space. As we know, we can calculate the area of any triangle either by Heron’s formula or the general formula. Both the formula will yield the same result. So, we can calculate the area of an isosceles triangle by the following methods:

General Formula

Basically, the area of an isosceles triangle is equal to half the product of its base and perpendicular height. The formula is illustrated below.

Area= ½*base*height

Heron’s Formula

Heron’s formula is used to calculate the area of a triangle if the dimensions of all its three sides are known. In the case of an isosceles triangle, the area by Heron’s formula is given by :

Area= √s(s-a)(s-b)(s-c)

Where, a, b, and c= three sides of an isosceles triangle

              S= (a+ b+ c)/2

As in isosceles triangles, two sides are equal,

Let us assume b=c

Then the modified Heron’s formula for an isosceles triangle becomes:

Area= √s(s-a)(s-b)(s-b)

Area= √s(s-a)(s-b)²

Area= (s-b) √s(s-a)

Some Formulas related to the Isosceles Triangle

Every geometrical shape has some associated features which can be expressed in the form of formulas. These formulas help to quickly solve the questions regarding those geometrical shapes. Some of the formulas regarding the Isosceles triangle are listed below.

• Perimeter = 2a+b, where a is the measure of equal sides and b is the measure of an unequal side
• Area= ½*b*h
• Area using Heron’s formula= (S-b) √S (S-a), where b is the length of equal sides and a is the length of an unequal side
• Height= √(a²-b²/4), where a is the measure of equal sides and b is the measure of an unequal side.

Types of Isosceles Triangle

The dimensions of an isosceles triangle are its legs, base, and height. All isosceles triangles show an axis of symmetry along the perpendicular bisector of the base. The angles between the legs are the sole factor upon which the isosceles triangles have been classified into different types. There are basically three types of isosceles triangle. These types are namely, Isosceles acute triangle, Isosceles right triangle, and Isosceles obtuse triangle. Let us dive deep into the details of these three types.

Isosceles Acute Triangle

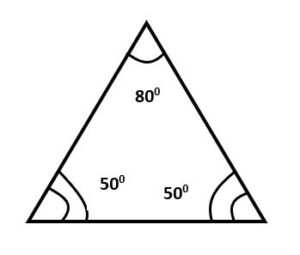
Isosceles acute triangles are those triangles whose two angles opposite the legs are equal and less than 90 degrees (acute angle). The third unequal angle in these triangles is always bigger than the other two equal angles.

Example of Isosceles Acute Triangle:

Isosceles Right Triangle

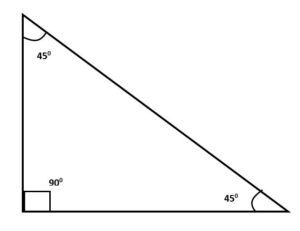
An Isosceles right triangle has two equal sides and two equal angles. The unequal angle is always 90° in this type of triangle. One of the two equal sides can act as perpendicular and the other side can act as base interchangeably. The third side is known as hypotenuse. So, we can say that this type of triangle satisfies the famous Pythagoras theorem.

Example of Isosceles right triangle:

Isosceles Obtuse Triangle

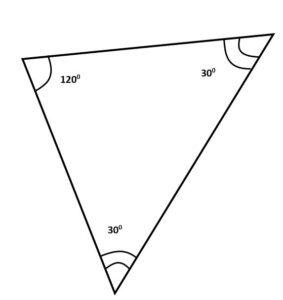
As we know in the case of triangles, there can’t be two angles more than 90° (obtuse angle). Isosceles obtuse triangles are those triangles whose two sides and two angles are equal and the unequal angle is obtuse, i.e., more than 90°.

Example of Isosceles Obtuse Triangle:

After learning these facts and formulas related to an Isosceles triangle, you will be able to easily able to answer all your queries related to Isosceles Triangles.

Sharing is caring!