CBSE Class 12 Maths Additional Practice Question Paper 2023-24

The Class 12 Maths Additional Practice Questions Paper 2023-24 for all students of Class 12 who have chosen PCM as their major stream has been released at the official website of the Central Board of Secondary Education www.cbseacademic.nic.in. The students preparing for the CBSE Class 12 Maths exam which is scheduled on March 09, 2024 must download and practice the CBSE Class 12 Maths Additional Practice Paper 2023-24 pdf thoroughly before attempting the actual board exam. As these sample papers will help them to understand and familiarize themselves with the actual board exam pattern and real exam-level questions. We have mentioned the CBSE Class 12 Maths Additional Practice Question Paper 2023-24 below in the article.

CBSE Class 12 Mathematics Sample Paper 2024 with Solutions

The CBSE Sample Paper for Class 12th Mathematics has a similar paper pattern to the CBSE Class 12th Mathematics Question Paper 2024. The Mathematics sample paper comprises different Five different sections: Section A, Section B, Section C, Section D, and Section E. The total marks for the CBSE class 12  Mathematics exam will be 100 marks out of which the Mathematics theory paper will be 80 marks while the rest 20 marks will be provided for the internal assessments.

CBSE Class 12th Mathematics Sample Paper 2024
Exam Conducting Body	Central Board of Secondary Education
Name of the Examination	CBSE Class 12th Board Examination 2024
Category	Sample Paper
Status	Released
CBSE Class 12th Maths Exam Date 2024	March 09, 2024
Mode of Sample Paper Availability	Online Mode
Official Website	www.cbseacademic.nic.in

CBSE Class 12 Maths Additional Practice Question Paper 2023-24

The newly updated CBSE Class 12 Additional Practice Question Papers 2023-24 are derived from the entire syllabus. It also consists of  50% competency questions, which might help the students in their further studies too. The Class 12 Maths Additional Practice Question Paper 2023-24 provides an overview of the board pattern, including the number of questions, types of questions (MCQs, Short answer, Long answer), time duration, and overall structure of the actual question paper. The Class 12 Maths Practice Question paper consists of a total of five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.

1. There are 18 Multiple-Choice Questions and 02 Assertion-Reason-based questions carrying 1 mark each in Section A.
2. 05 Very Short Answer (VSA)-type questions carrying 02 marks each in Section B.
3. Section C consists of 06 Short Answer (SA)-type questions carrying 03 marks each.
4. 04 Long Answer (LA)-type questions of 05 marks each are present in Section D.
5. Section E consists of 03 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with sub-parts.

Maths Additional Practice Question Paper 2023-24 CBSE Class 12

Now the students appearing for the Class 12th board exams for the session 2023-24 can download the CBSE Class 12 Maths Additional Practice Question Paper 2023-24 pdf with their solutions and marking scheme from the direct link mentioned below. As these practice papers will help the students to understand and familiarize themselves with the newly upgraded format of class 12 board exams. The class 12th students are advised to go through these sample papers to familiarize themselves with the types of questions that can be asked in the actual examination.

CBSE Class 12 Maths Additional Practice Question Paper 2023-24 PDF
Additional Practice Question Paper 2023-24 PDF	Solution Pdf
Class 12 Maths Practice Question Paper 2023-24	Solution Link

Class 12 Maths Addition Practice Paper 2023-24

Below we have discussed the complete CBSE Class 12th Mathematics Additional Practice Paper 2023-24 with solutions.

Section A – Multiple Choice Questions

Q1. For any 2 × 2 matrix P, which of the following matrices can be Q such that PQ = QP?

Ans: (b)

Q2. V is a matrix of order 3 such that |adj V| = 7.
Which of these could be |V|?

(a)- 7²

(b)- 7

(c)- √7

(d)- ³√7

Ans: (c) √7

Q3: The points D, E, and F are the mid-points of AB, BC, and CA respectively.

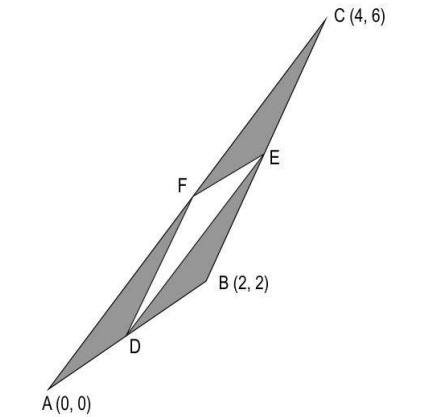(Note: The figure is not to scale.)

What is the area of the shaded region?
(a) 2 sq units
(b) 3/2 sq units
(c) 1/2 sq units
(d) (2√26 – 1) sq units

Ans: (b) 3/2 sq units

Q4: If f(x) = cos-1√x, 0 < x < 1, which of the following is equal to F (x)?

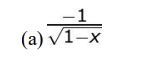
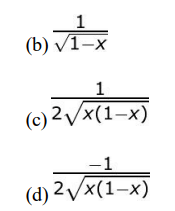
Ans: (d)

Q5: A function f: R -> R is defined by: 

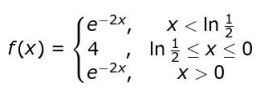
Which of the following statements is true about the function at the point x = ln 1/2?
(a) f(x) is not continuous but differentiable.
(b) f(x) is continuous but not differentiable.
(c) f(x) is neither continuous nor differentiable.
(d) f(x) is both continuous as well as differentiable.

Ans: (b) f(x) is continuous but not differentiable.

Q6. In which of these intervals is the function f(x) = 3x² – 4x strictly decreasing?
(a) (-∞, 0)
(b) (0, 2)
(c) (2/3, ∞)
(d) (-∞, ∞)

Ans: (a) (-∞, 0) 

Q7. Which of these is equal to ∫ 𝑒^{(𝑥log 5)} 𝑒^𝑥𝑑𝑥, where C is the constant of integration?

(a) (5e)^𝑥/log 5e + C

(b) log 5^𝑥 + x + C

(c) 5^𝑥e^𝑥 + C

(d) (5e)^𝑥 log x + C

Ans: (5e)^𝑥/log 5e + C

Q8. Shown below is the curve defined by the equation y = log (x + 1) for x ≥ 0.

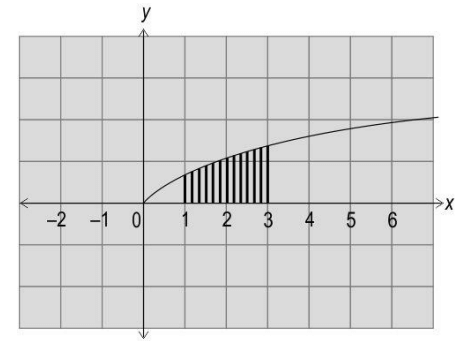
Which of these is the area of the shaded region?
(a) 6log(2) – 2
(b) 6log(2) – 6
(c) 6log(2)
(d) 5log(2)

Ans: (a) 6log(2) – 2

Q9. In which of the following differential equations is the degree equal to its order?

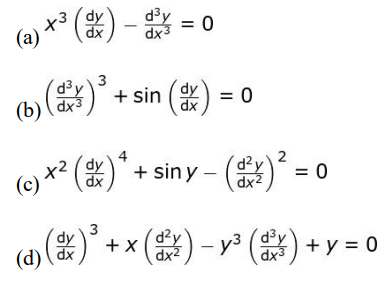
Ans: (c)

Q10. Kapila is trying to find the general solution of the following differential equations.

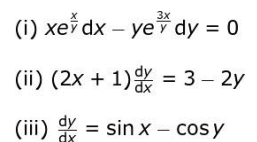
Which of the above becomes variably separable by substituting y = b.x, where b is a variable?
(a) only (i)
(b) only (i) and (ii)
(c) all – (i), (ii) and (iii)
(d) None of the above.

Ans: (a) only (i).

Q11. For which of these actors is the projection on the y-axis zero?

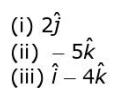
(a) only (i)
(b) only (ii)
(c) only (i) and (ii)
(d) only (ii) and (iii)

Ans: (d) only (ii) and (iii)

Q12.

 

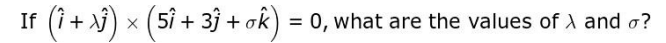
(a) λ = 3/5, σ = 0
(b) λ = 5/3, σ = 5
(c) λ = 3, σ = 0
(d) (cannot be found as there are two unknowns and only one equation)

Ans: (a) λ = 3/5, σ = 0

Q13.

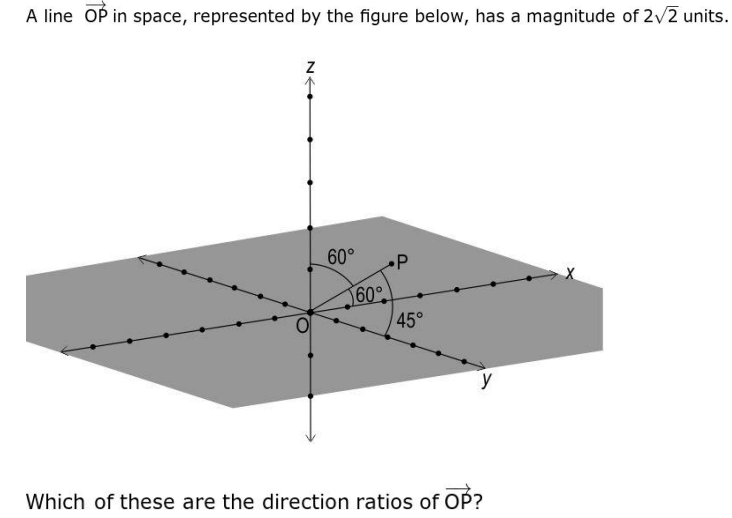
(a) (2, √2, 2)
(b) (√2, 2, √2)
(c) (1/2, 1/√2, 1/2)
(d) (2√2, 2√2, 2√2)

Ans: (b) (√2, 2, √2)

Q14. A line m passes through the point (-4, 2, -3) and is parallel to line n, given by:

(-x-2)/4 = (y + 3)/-2 = (2z-6)/3

The vector equation of line m is given by:

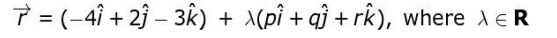
Which of the following could be the possible values for p, q, and r?
(a) p = 4, q = (-2), r = 3
(b) p = (-4), q = (-2), r = 3
(c) p = (-2), q = 3, r = (-6)
(d) p = 8, q = 4, r = (-3)

Ans: (d) p = 8, q = 4, r = (-3)

Q15. L1 and L2 are two skew lines. 

How many lines joining L1 and L2 can be drawn such that the line is perpendicular to both L1 and L2?

(a) exactly one
(b) exactly two
(c) infinitely many
(d) (there cannot be a line joining two skew lines such that it is perpendicular to both).

Ans: (a) exactly one.

Q16. A linear programming problem (LPP) along with the graph of its constraints is shown below. The corresponding objective function is Minimize: Z = 3x + 2y. The minimum value of the objective function is obtained at the corner point (2, 0).

The optimal solution of the above linear programming problem _________.
(a) does not exist as the feasible region is unbounded.
(b) does not exist as the inequality 3x + 2y < 6 does not have any point in common with the feasible region.
(c) exists as the inequality 3x + 2y > 6 has infinitely many points in common with the feasible region.
(d) exists as the inequality 3x + 2y < 6 does not have any point in common with the feasible region.

Ans: (d) exists as the inequality 3x + 2y < 6 does not have any point in common with the feasible region. 

Q17. The feasible region of a linear programming problem is bounded. The corresponding objective function is Z = 6x – 7y.

The objective function attains __________ in the feasible region.
(a) only minimum
(b) only maximum
(c) both maximum and minimum
(d) either maximum or minimum but not both.

Ans: (c) both maximum and minimum.

Q18. M and N are two events such that P(M ∩ N) = 0.

Which of the following is equal to P(M|(M ∪ N))?

(a) P (M)/ P (N)

(b) P (M∪N)/P (M∪N)

(c) P (M)/P (M) + P (N)

(d) P (M)/P (M) × P(N)

Ans: (c) P (M)/P (M) + P (N)

Q19. X = {0, 2, 4, 6, 8}.
P is a relation on X defined by P = {(0, 2), (4, 2), (4, 6), (8, 6), (2, 4), (0, 4)}.

Based on the above information, two statements are given below – one labeled Assertion (A) and the other labeled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).

Assertion (A): The relation P on set X is a transitive relation.
Reason (R): The relation P has a subset of the form {(a, b), (b, c), (a, c)}, where a, b, c ∈ X.

(a) Both (A) and (R) are true and (R) is the correct explanation for (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Ans: (d) (A) is false but (R) is true.

Q20. Two statements are given below – one labeled Assertion (A) and the other labeled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R). 

Assertion (A): The maximum value of the function f(x) = x⁵, x ∈ [-1, 1], is attained at its critical point, x = 0.
Reason (R): The maximum of a function can only occur at points where the derivative is zero.

(a) Both (A) and (R) are true and (R) is the correct explanation for (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(c) (A) is false but (R) is true.
(d) Both (A) and (R) are false.

Ans: (d) Both (A) and (R) are false.

Section B – Very Short Answer Questions

Q21. Find the domain of the function y = cos^–¹(|x – 1|). Show your steps. 

Solution: Since the domain of the inverse of the cosine function is [-1, 1], find the domain of the given function as follows:

-1 ≤ x – 1 ≤ 1
So, 0 ≤ x ≤ 2

And,
-1 ≤ 1 – x ≤ 1
=> 1 ≥ x – 1 ≥ -1
So, 2 ≥ x ≥ 0
Concludes the domain of cos^–¹(|x – 1|) as [0, 2].

OR

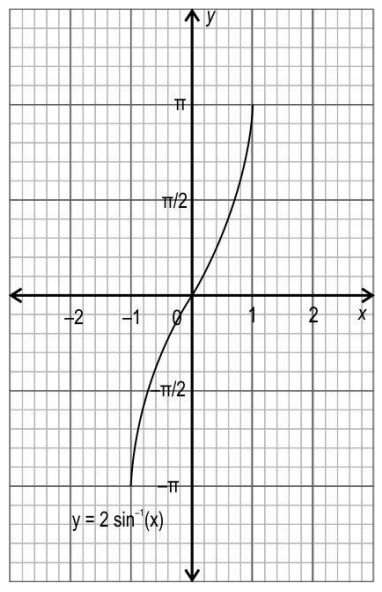
Q21. Draw the graph of the following function:
y = 2sin^–¹(x), -π ≤ y ≤ π

Solution: Draws the graphs of y = 2sin^–¹(x) as shown below.

Q22.

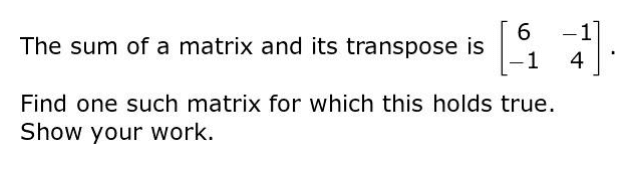
Solution:

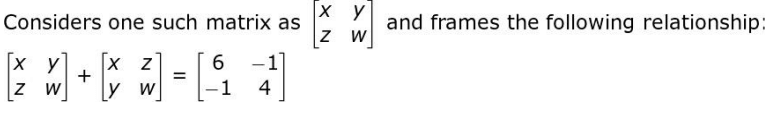
Obtains x = 3 and w = 2 using the relationship obtained in the previous step as
follows:
2x = 6 => x = 3
2w = 4 => w = 2
Writes any value of y and z that satisfies the third relationship obtained in the first
step. For example, y = 0 and z = -1.

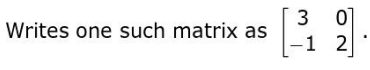
(Award full marks for any other matrix that satisfies the relationship.)

Q23. If x = cot t and y = cosec²t, find:

(i) dy/dx

(ii) d²y/dx²

Show your steps.

Solution:

(Award full marks if any alternate method is used.)

Q24. Iqbal, a data analyst in a social media platform is tracking the number of active users on their site between 5 pm and 6 pm on a particular day.

The user growth function is modeled by N(t) = 1000e^0.1t, where N(t) represents the number of active users at time t minutes during that period.

Find how fast the number of active users are increasing or decreasing at 10 minutes past 5 p.m. Show your steps.

Solution: Writes that the rate at which the number of active users is increasing or decreasing at a given time is given by 𝑑/𝑑𝑡N(t).

Finds the derivative of N(t) as:

𝑑/𝑑𝑡N(t) = 1000 (0.1) e^0.1t

Finds the rate of change of active users at 10 minutes past 5 pm as:

𝑑/𝑑𝑡N(10) = 1000(0.1)e^(0.1)(10) = 100e
Concludes that the number of active users are increasing at a rate of 100e people per minute at 5:10 pm on that day.

OR

Q24. The population of rabbits in a forest is modeled by the function below:

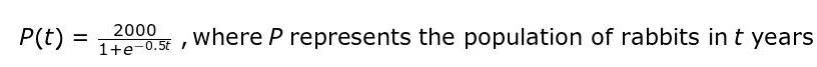
Determine whether the rabbit population is increasing or not, and justify your answer.

Solution: Find the derivative of the given function as:

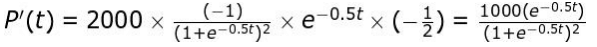
Writes that the above quantity is greater than 0 for any value of t.
Concludes that the rabbit population is increasing.

Q25. Solve the integral: 

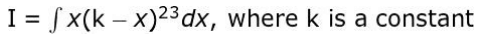
Show your steps.

Solution: Substitutes (k – x) by u to get dx = -du and rewrites the given integral as:

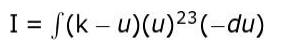
Integrates the expression in the above step as:

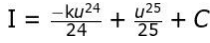
where C is the constant of integration

Substitute u = (k – x) back in the above expression and write:

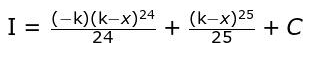
where C is the constant of integration.

Section C – Short Answer Type Questions

Q26. Solve the integral:

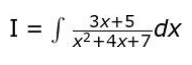
Show your work.

Solution: Rewrites the numerator of the given integral as:
3x + 5 = A 𝑑/𝑑𝑥(x² + 4x + 7) + B
=> 3x + 5 = A(2x + 4) + B
Finds the values of A and B by comparing the coefficients of like terms as:
2A = 3 => A = 3/2
4A + B = 5 => B = -1
Substitutes the values of A and B in the given integral and integrates the same as:

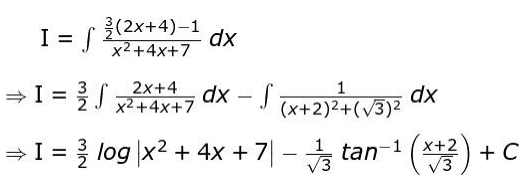
where C is the constant of integration.

Q27. Evaluate the integral:

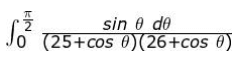
Show your steps.

Solution: Takes u = (25 + cos θ).
Finds du as:
du = -sin θ dθ
Finds the change in limit when θ = 0 and θ = 𝜋/2 to u = 26 and u = 25 respectively

Rewrites the given integral using the above substitution and integrates the same as:

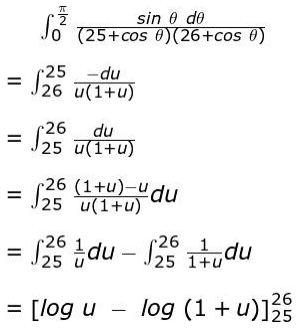
Applies the limit to find the value of the given definite integral as log 26 ×26/25 ×27

(Award full marks if the problem is solved correctly by taking u = 26 + cos θ.)

OR

Q27. Using the properties of definite integrals, prove the following:

State the property used.

Solution: States the property that is going to be used as:

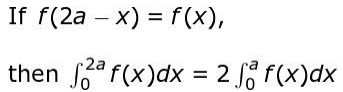
Takes 2a = π and f(x) = h(sin x).
Finds f(2a – x) as:
f(2a – x) = f(π – x) = h(sin(π – x)) = h(sin x) = f(x)

Thus confirms that the property listed in the above step can be applied to the given integral.
Hence concludes that:

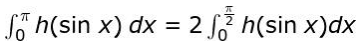
Q28. When an object is thrown vertically upward, it is under the effect of gravity and air resistance. For small objects, the force due to air resistance is numerically equal to some constant k times v, where v is the velocity of the object (in m/s) at time t (s).

This situation can be modeled as the differential equation shown below.

A tennis ball of mass 0.050 kg is hit upwards with a velocity of 10 m/s. An air resistance numerically equal to 0.4v acts on the ball.

(i) Model the above situation using a differential equation.
(ii) Write an expression for the velocity of the ball in terms of time.

Show your work.

Solution: (i) Models the situation and rearranges terms to form a linear differential equation as follows:

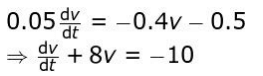
(ii) Considering the obtained equation as linear of the form 𝑑𝑦/𝑑𝑥 + Py = Q with P = 8 and hence takes the integrating factor as:

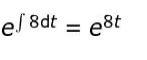
Multiplies the differential equation by the integrating factor as follows:

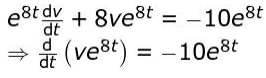
Integrates both sides to obtain the general solution of the differential equation as follows:

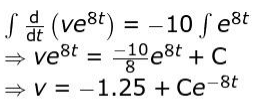
Where C is the constant of integration.

Uses the initial condition v(0) = 10 m/s to find the value of C as follows:

10 = -1.25 + C

⇒C = 11.25

Hence, write the expression for the velocity of the ball as a function of time as follows:

v = -1.25 + 11.25e^-8t

Q29. Shown below is a curve.

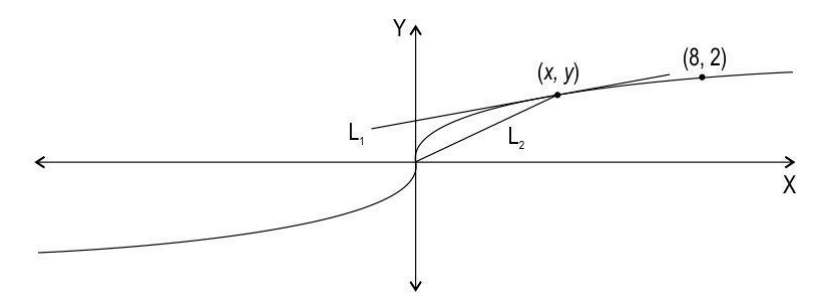
L₁ is the tangent to any point (x, y) on the curve.
L₂ is the line that connects the point (x, y) to the origin.

The slope of L₁ is one-third of the slope of L₂.
Find the equation of the curve. Show your work.

Solution: Frames the differential equation using the given conditions as follows:

dy/dx = 1/3 × y/x

⇒ dy/dx = y/3x

Rearrange the terms to separate the variables as follows:

dy/y = dx/3x

Integrates both sides to obtain the general solution of the curve. The working may look as follows:

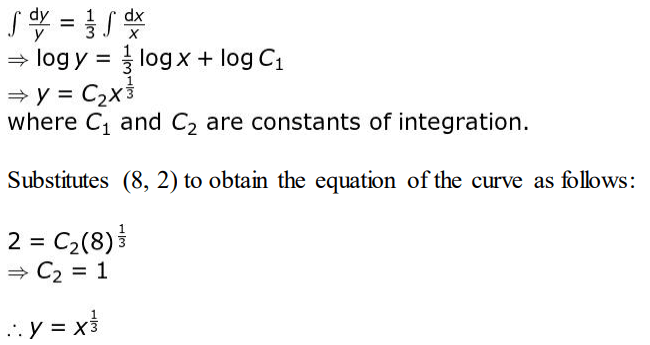
OR

Q29. Given x + (y +1) dy/dx = 2

(i) Solve the differential equation and show that the solution represents a family of circles.
(ii) Find the radius of a circle belonging to the above family that passes through the origin.

Show your work.

Solution: (i) Separate the variables and rearrange the terms of the differential equation as follows:

x = (y = 1) dx/dy = 2

⇒ (y + 1) dy = (2 – x) dx

Integrates both sides to obtain the following:

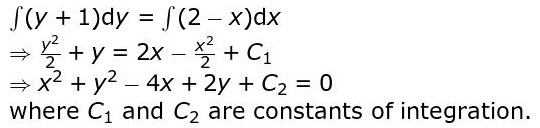
Writes that the solution is a general solution of a circle and hence it represents a family of circles.
(ii) Substitutes x = 0 and y = 0 into the general solution to obtain C2 = 0 and writes the particular solution as:
x² + y² – 4x + 2y = 0

Rearrange the terms to rewrite the particular solution as (x – 2)² + (y + 1)²= 5 to find the radius as √5 units. The working may look as follows:
x² + y² – 4x + 2y = 0
Adding 5 to both sides and rearranging terms,
=> (x² – 4x + 4) + (y² + 2y + 1) = 5
=> (x – 2)² + (y + 1)² = 5

Q30. Each unit of Product A that a company produces is sold for Rs 100 with a production cost of Rs 60 and each unit of Product B is sold for Rs 150 with the production cost of Rs 90. On a given day, the company has a budget of Rs 8000 to spend on production. The production process makes it such that they can only produce a maximum of 100 units each day. Also, the number of Product B produced cannot be more than twice as many of Product A.

Frame a linear programming problem to determine how many units of Products A and B should the company produce in a day in order to maximize its profit.

(Note: No need to find the feasible region and optimal solution.)

Solution: Finds the profit on selling the products as:

Profit for each unit of Product A sold = 100 – 60 = Rs 40
Profit for each unit of Product B sold = 150 – 90 = Rs 60.

Takes x and y to be the numbers of Product A and Product B to be produced in a day respectively and frames the objective function as:
Maximise Z = 40x + 60y

Writes the constraints of the given linear programming problem as:
60x + 90y ≤ 8000
x + y ≤ 100
y ≤ 2x or -2x + y ≤ 0
x, y ≥ 0.

OR

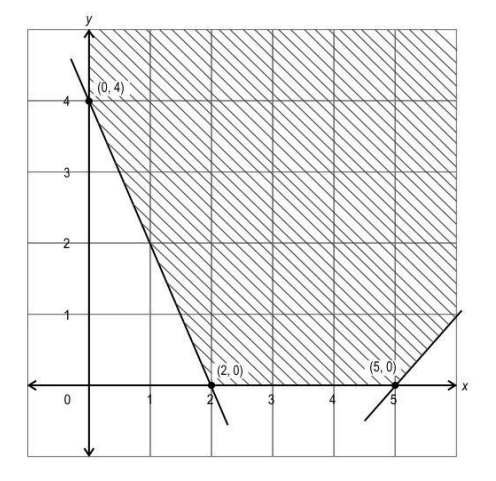
Q30. Shown below is the feasible region of a maximization problem whose objective function is given by Z = 5x + 3y. 

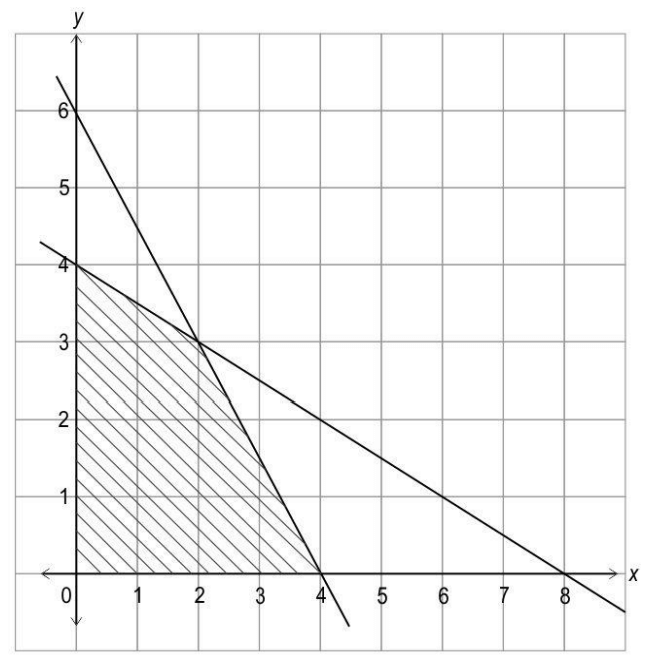
i) List all the constraints the problem is subjected to.
ii) Find the optimal solution of the problem.

Show your work.

Solution: i) Uses the graph of the feasible region and lists the constraints of the given maximization problem as:
3x + 2y ≤ 12
x + 2y ≤ 8
x, y ≥ 0

ii) Finds the value of the objective function at corner points as:

Corner Point	z = 5x + 3y
(0,0)	0
(0,4)	12
(2,3)	19
(4,0)	20

Concludes that the objective function attains maximum value at (4, 0) and hence (4, 0) is the optimal solution.

Q31. A company follows a model of bifurcating the tasks into the categories shown below.

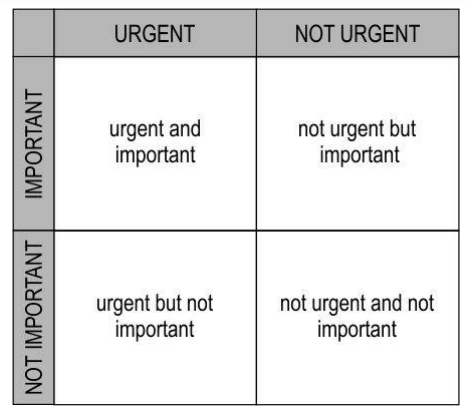
At the beginning of a financial year, it was noticed that:

♦ 40% of the total tasks were urgent and the rest were not.
♦ half of the urgent tasks were important, and
♦ 30% of the tasks that were not urgent, were not important

What is the probability that a randomly selected task that is not important is urgent? Use Bayes’ theorem and show your steps.

Solution: Applies Bayes’ theorem and writes:

P (Urgent/Not Important) = [P (Urgent) × P (Not important/Urgent)] ÷ [P(Urgent) × P (Important/Urgent) + P (Not urgent) × P (Noy important/Not urgent)]

Substitute respective probabilities in the expression obtained above to find the required probability as follows:

Simplifies the above expression to get the probability that a randomly selected task that is not important is urgent as 10/19 or 52.63%.

Section D – Long Answer Questions

Q32. The Earth has 24 time zones, defined by dividing the Earth into 24 equal longitudinal segments. These are the regions on Earth that have the same standard time. For example, the USA and India fall in different time zones, but Sri Lanka and India are in the same time zone.

A relation R is defined on the set U = {All people on the Earth} such that R = {(x, y)| the time difference between the time zones x and y reside in is 6 hours}.

i) Check whether the relation R is reflexive, symmetric or transitive.
ii) Is relation R an equivalence relation?

Show your work.

Solution: i) Writes that for no x ∈ U, (x, x) ∈ R as the difference in time between x & x is 0 hours.

Concludes that R is not reflexive.
Writes that, whenever the difference in time between x and y is 6 hours, the difference in time between y and x is also 6 hours. That is, (x, y) ∈ R => (y, x) ∈ R.

Concludes that R is symmetric.
Writes that, if the difference in time between x and y is 6 hours, and the difference in time between y and z is also 6 hours, then the difference in time between x and z could be either 0 hours or 12 hours. That is, (x, y) ∈ R & (y, z) ∈ R but (x, z) ∉ R.

Concludes that R is not transitive.

ii) From the above steps, concludes that R is not an equivalence relation.

OR

Q32. A function f : R – {-1, 1} -> R is defined by:

f (x) = x / x² – 1

i) Check if f is one-one.
ii) Check if f is onto.

Show your work.

Solution: i) Assumes f(x) = f(y) and evaluates the same as:

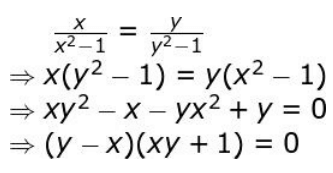
Uses the above step to conclude that x = y or xy = -1.
Takes a pair of numbers x and y such that xy = -1 to show that f is not one-one.
For example,
for x = 1/2 and y = -2, f(x) = − 2/3 and f(y) = − 2/3.

ii) Equates f(x) to y and solves the same to express x in terms of y as:

Writes that for any y ∈ R (codomain), there exists x ∈ R – {-1, 1} (domain) such that f(x) = y. Hence concludes that f is onto.

Q33. Abdul threw a basketball in the direction of the basketball hoop which traversed a parabolic path in a vertical plane as shown below.

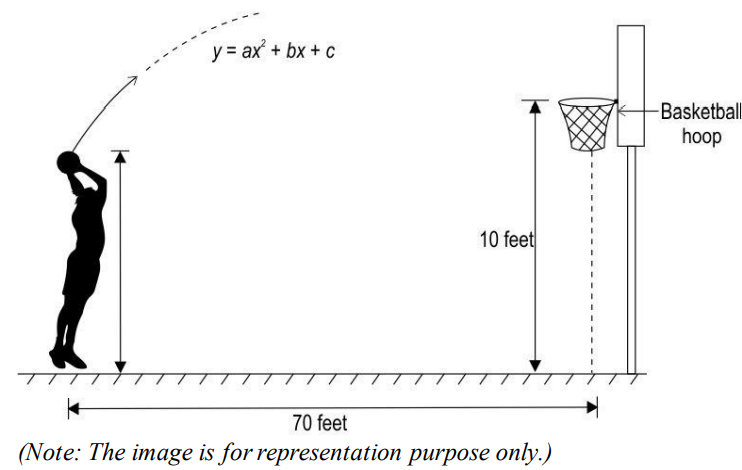
The equation of the path traversed by the ball is y = ax2 + bx + c with respect to a xy-coordinate system in the vertical plane. The ball traversed through the points (10, 16), (20, 22) and (30, 25). The basketball hoop is at a horizontal distance of 70 feet from Abdul. The height of the basketball hoop is 10 feet from the floor to the top edge of the rim.

Did the ball successfully go through the hoop? Justify your answer.

(Hint: Consider the point where Abdul is standing as the origin of the xy-coordinate system.)

Solution: Writes the system of equations as:
100a + 10b + c = 16
400a + 20b + c = 22
900a + 30b + c = 25
Writes the above system of equations in the form AX = B as:

(Award 1 mark if only all the cofactors are found correctly.)

Finds the values of a, b and c as −
3/200, 21/20and 7 respectively by solving
X = A^-1B as:

Finds the equation of the path traversed by the ball as:
y = − 3/200 x² + 21/20 x + 7.
Writes that when x = 70 feet, y = 7 feet. So, the ball went by 7 feet above the floor which means 3 feet below the basketball hoop. So, the ball did not go through the hoop.

Q34. Shown below are concrete elliptical water pipes, each 10 feet in length.

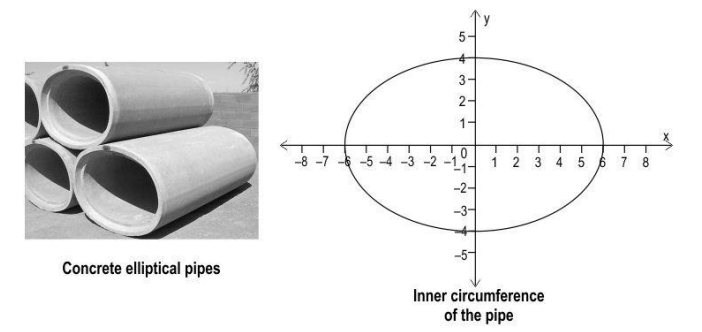
The graph given above represents the inner circumference of the elliptical pipe, where x and y are in feet. Assume that the water flows uniformly and fully covers the inner cross-sectional area of the pipe.

Find the volume of water in the pipe at a given instant of time, in terms of π.
Use the integration method and show your steps.

(Note: Volume = Area of the base × Height)

Solution: Finds the equation of the ellipse as:

x²/36 + y²/16 = 1

Expresses y in terms of x as:

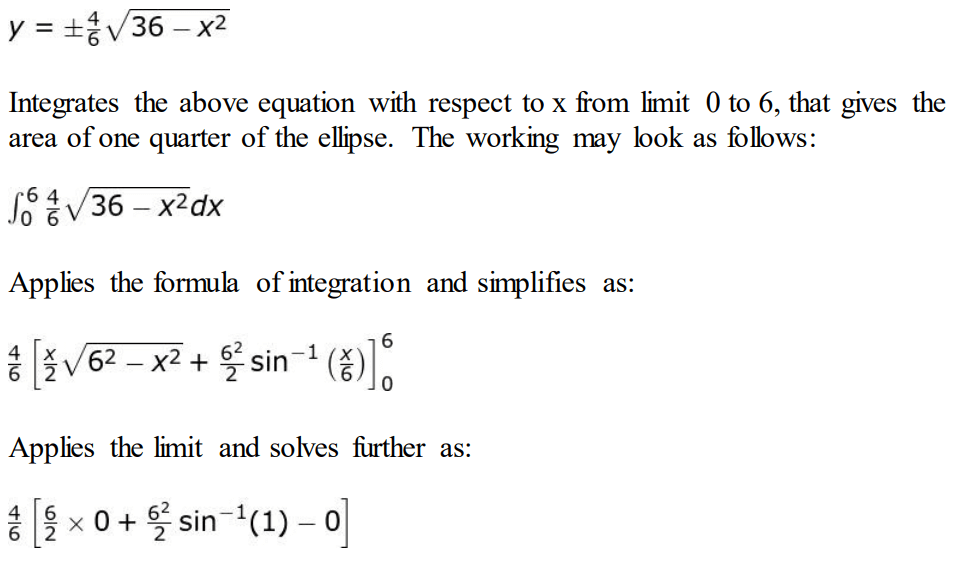
Simplifies the above expression to get the area of one-quarter of the base as 6π sq feet.
Finds the area of the whole ellipse as 4 × 6π = 24π sq feet.
Finds the volume of water as 24π × 10 = 240π cubic feet.

Q35. i) Find the vector and cartesian equations of the straight line passing through the point (-5, 7, -4) and in the direction of (3, -2, 1).
ii) Find the point where this straight line crosses the xy-plane.

Show your work.

Solution:

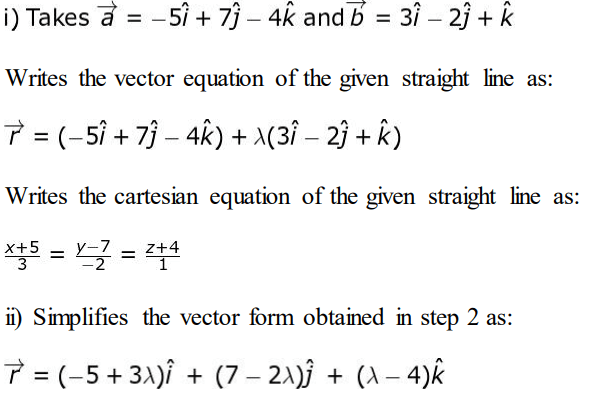
Writes that at the point where the line crosses the xy-plane, its z-coordinate is zero and equates the z-coordinate of the above equation to zero as:
λ – 4 = 0
=> λ = 4
Substitutes λ = 4 in the vector form to get the required point as (7, -1, 0).

OR

Q35. Given below are two lines L1 and L2:
L1: 2x = 3y = -z
L2: 6x = -y = -4z

i) Find the angle between the two lines.
ii) Find the shortest distance between the two lines.

Show your work.

Solution: Rewrites the equation of L1 in cartesian form as:
𝑥/3 = 𝑦/2 = 𝑧/−6
Rewrites the equation of L2 in cartesian form as:
𝑥/2 = 𝑦/−12 = 𝑧/−3

i) Identifies the direction cosines of both the lines as (3, 2, -6) and(2, -12, -3).

Finds the cosine of the angle between the two lines as:

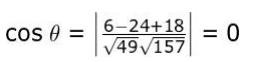
(Award 0.5 marks if only the formula of the cosine of the angle between the two lines is written correctly.)
Concludes that the angle between the two lines is 90°.

ii) Rewrites the equations of L1 and L2 in vector form as:

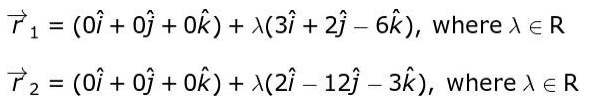
Writes that both the lines pass through the origin and hence intersect at the origin.

(Award full marks if the inference about both lines passing through the origin is drawn without writing the vector forms.)

Writes that since both the lines intersect at the origin, the shortest distance between the two lines is 0 units.

Section E – Case Study Questions

Q36. Answer the questions based on the given information.

The flight path of two airplanes in a flight simulator game are shown below.
The coordinates of the airports P and Q are given.

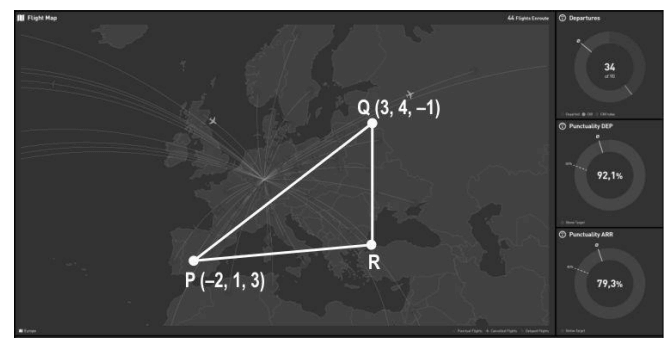
Airplane 1 flies directly from P to Q.
Airplane 2 has a layover at R and then flies to Q.

(Note: Assume that the flight path is straight and fuel is consumed uniformly throughout the flight.)

i) Find the vector that represents the flight path of Airplane 1. Show your steps.

ii) Write the vector representing the path of Airplane 2 from R to Q. Show your steps.

iii) What is the angle between the flight paths of Airplane 1 and Airplane 2 just after takeoff? Show your work.

OR

iii) Consider that Airplane 1 started the flight with a full fuel tank.
Find the position vector of the point where a third of the fuel runs out if the entire fuel is required for the flight. Show your work.

Solution: (i) Writes the vectors for points P and Q as follows:

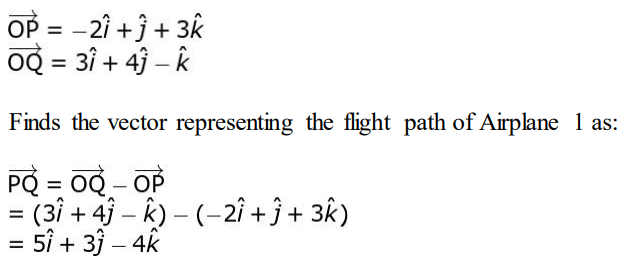
(ii) Uses vector subtraction to find the vector representing the flight path from R to Q as:

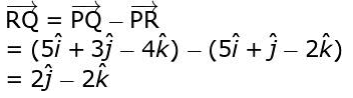
(iii) Finds the cosine of the angle between the vectors representing the flight paths of Airplane 1 and Airplane 2 as:

OR

(iii) Considers a point S which divides PQ internally in the ratio 1:2.
Finds the position vector of point S as:

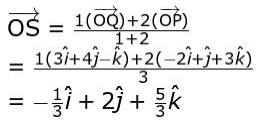
(Award 0.5 marks if only the formula is written correctly.)

Q37. Answer the questions based on the given information.
Rubiya, Thaksh, Shanteri, and Lilly entered a spinning zone for a fun game, but there is a twist: they don’t know which spinner will appear on their screens until it is their turn to play. They may encounter one of the following spinners, or perhaps even both:

 

Different combinations of numbers will lead to exciting prizes. Below are some of the rewards they can win:
♦ Get the number ‘5’, from Spinner A and ‘8’ from Spinner B, and you’ll win a music player!
♦ You win a photo frame if Spinner A lands on a value greater than that of Spinner B!

i) Thaksh spun both the spinners, A and B in one of his turns.
What is the probability that Thaksh wins a music player in that turn? Show your steps.

ii) Lilly spun spinner B in one of her turns.
What is the probability that the number she got is even given that it is a multiple of 3? Show your steps.

iii) Rubiya spun both the spinners.
What is the probability that she wins a photo frame? Show your work.

OR

iii) As Shanteri steps up to the screen, the game administrator reveals that for her turn, the probability of seeing Spinner A on the screen is 65%, while that of Spinner B is 35%.
What is the probability that Shanteri gets the number ‘2’? Show your steps.

Solution: (i) Finds the required probability as:

P (5 from spinner A) ∩ P (8 from spinner B)

= 1/4 × 1/8

= 1/32

(ii) Uses the conditional probability and finds the required probability as follows:

P (Even / Multiple of 3)

= P (Even ∩ Multiple of 3) ÷ P(Multiple of 3)

= 1/8 ÷ 2/8

= 1/2

(iii) Finds the probability of getting 2 from spinner A and getting 1 from spinner B as:

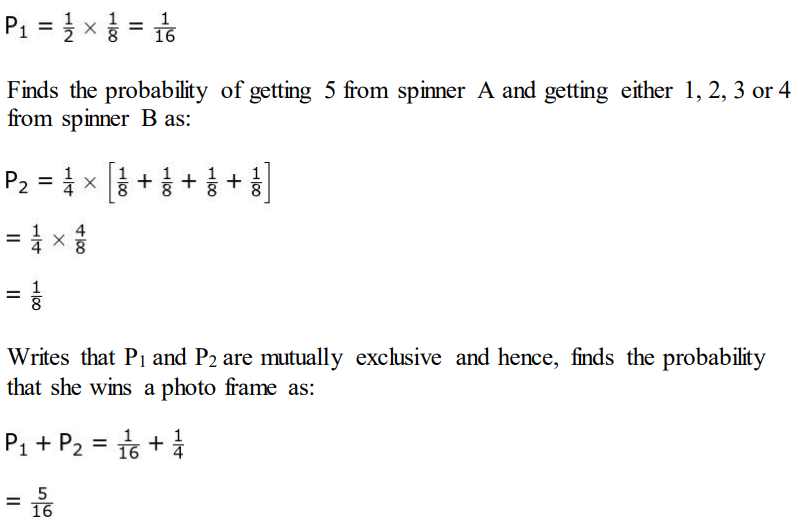
OR

(iii) Uses the theorem of total probability and writes:
P(getting 2) = [P(Spinner A) × P(Getting 2|Spinner A)] + [P(Spinner B) × P(Getting 2|Spinner B)]
Finds the required probability by substituting the required probability as:

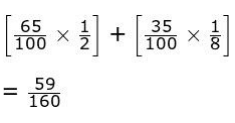
Q38. Answer the questions based on the given information.

Two metal rods, R1 and R2, of lengths 16 m and 12 m respectively, are insulated at both the ends. Rod R1 is being heated from a specific point while rod R2 is being cooled from a specific point.

The temperature (T) in Celsius within both rods fluctuates based on the distance (x) measured from either end. The temperature at a particular point along the rod is determined by the equations T = (16 – x)x and T = (x – 12)x for rods R1 and R2 respectively, where the distance x is measured in meters from one of the ends.

i) Find the rate of change of temperature at the mid point of the rod that is being heated. Show your steps. 
ii) Find the minimum temperature attained by the rod that is being cooled.

Show your work

Solution: (i) Identifies that the rod being heated is R1 and finds the rate of change of temperature at any distance from one end of R1 as:

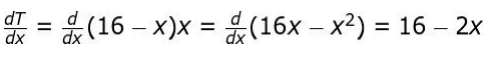
Find the mid-point of the rod as x = 8 m.
Finds the rate of change of temperature at the midpoint of R1 as:

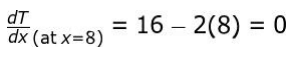
(ii) Identifies that the rod being cooled is R2 and finds the rate of change of temperature at any distance x m as:

Finds the minimum temperature attained by the rod R2 as
T(6) = (6 – 12)6 = -36 °C.

Related Links
CBSE Additional Practice Questions 2023-24 Class 12	CBSE Class 12 English Additional Practice Question Paper 2023-24
CBSE Class 12 Business Studies Additional Practice Question Paper 2023-24	CBSE Class 12 Chemistry Additional Practice Questions Paper 2023-24
CBSE Class 12 Biology Additional Paper 2023-24	CBSE Class 12 Physics Additional Practice Questions Paper 2023-24

Sharing is caring!