Rotational Motion Dynamics Class 12 Physics Notes

Define Rotational Motion

The rotational motion of a rigid body involves the spinning or turning of an entire object around a fixed point or axis. Unlike non-rigid bodies, rigid bodies maintain their shape during rotation. Picture a spinning top, where the entire object rotates as one solid unit. In the context of rigid body rotation, terms like moment of inertia become significant, representing an object’s resistance to changes in its rotational motion.

The axis of rotation plays a crucial role; it is the imaginary line about which the rigid body rotates. Applications of rigid body rotation are widespread, from understanding the dynamics of rotating machinery in engineering to describing celestial bodies’ rotational behavior in astronomy. Analyzing rotational motion in rigid bodies is fundamental in comprehending the physical principles governing various mechanical systems.

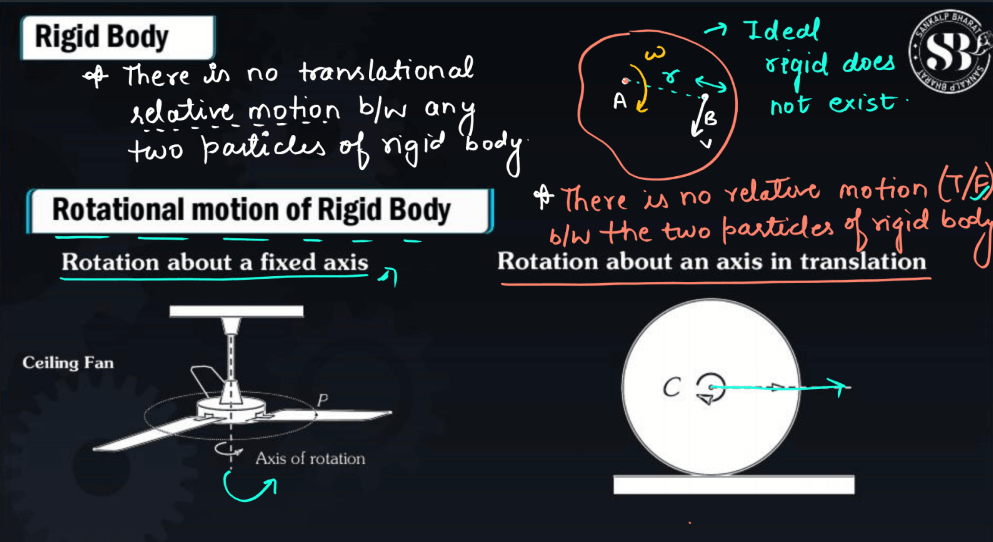
Rotational Motion About the Fixed Axis

Rotational motion around a fixed axis occurs when an object spins or turns in a circular manner without changing its position. Imagine a spinning top or a merry-go-round – these are examples of rotational motion. The fixed axis serves as an imaginary line around which the object rotates. The rate at which the object turns is called angular velocity, measured in degrees or radians per unit of time. Angular displacement represents how far the object has rotated from its starting position, usually measured in degrees or radians. Rotational motion involves torque, which is the force that causes the rotation, and moment of inertia, a measure of an object’s resistance to changes in its rotation. Understanding rotational motion is crucial in various fields, from physics and engineering to everyday activities like driving a car or riding a bicycle, where wheels rotate around their axes.

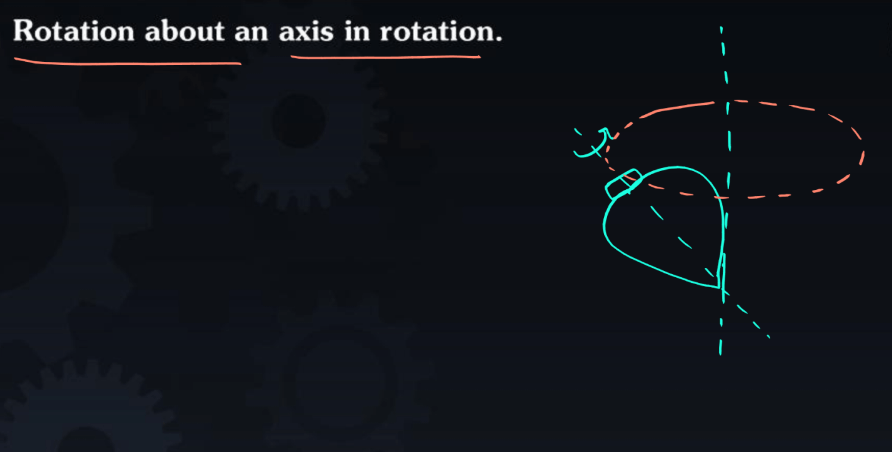
Rotation About an Axis in Transition

Rotation about an axis in transition refers to the spinning or turning motion of an object as it moves from one position to another, maintaining a fixed axis of rotation. Picture a spinning top that not only rotates but also changes its location over time. This concept combines both translational and rotational motion. In this scenario, the object not only travels in a straight line (translation) but also undergoes rotational movement around a specific axis. This combination of translational and rotational motion is often encountered in dynamic systems, such as a rolling wheel or a spinning globe moving across a surface. Understanding the interplay between translation and rotational motion is crucial in analyzing the overall motion of complex systems, providing insights into their behavior, and helping design efficient mechanisms in engineering and physics.

Moment of Inertia

The moment of inertia is a measure of an object’s resistance to changes in its rotation. Imagine spinning a bicycle wheel – the larger the wheel or the more mass it has concentrated toward the outer edges, the harder it is to start or stop the rotation. Moment of inertia qualifies this resistance. It depends on both the mass distribution and the shape of the object. For a simple analogy, consider opening a door: pushing near the hinges requires more effort than pushing at the outer edge. Similarly, in rotational motion, the moment of inertia reflects how the mass is distributed relative to the axis of rotation, affecting how easily or difficulty an object can spin.

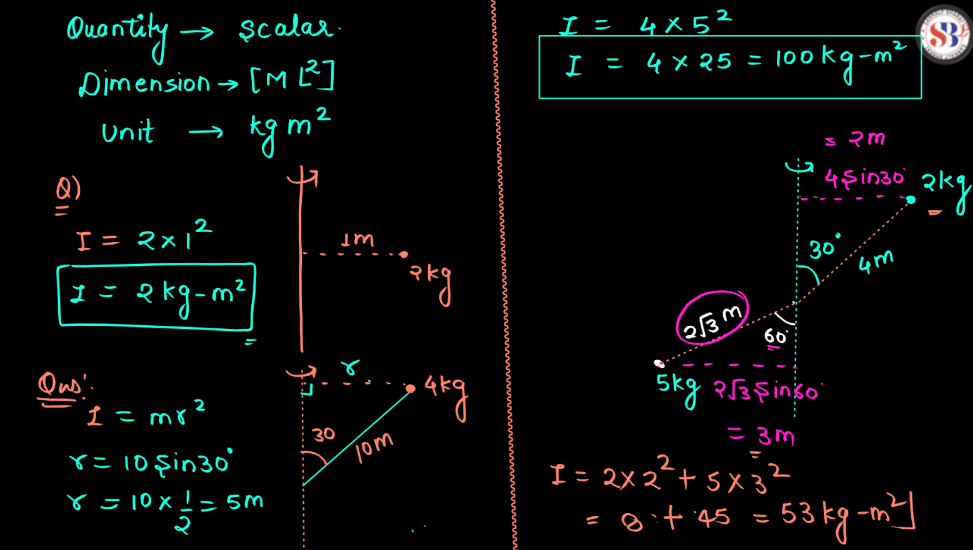
Radius of Gyration

The radius of gyration is a measure that describes how the mass of an object is distributed around its axis of rotation. In simpler terms, it indicates how spread out or concentrated the mass is within a rotational object. Imagine spinning a ball on your finger – if the mass is evenly distributed, it’s easier to balance. The radius of gyration quantifies this distribution, essentially providing a hypothetical distance from the axis where you could concentrate all the mass to produce the same rotational inertia. Mathematically, it’s the square root of the ratio of the moment of inertia to the total mass. A smaller radius of gyration implies more concentrated mass and can affect how an object responds to rotation.

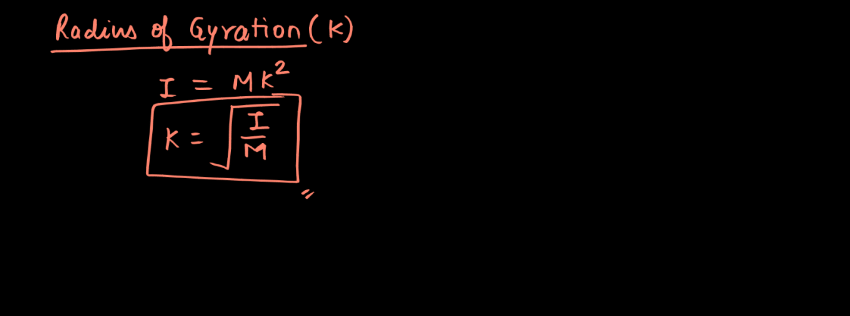
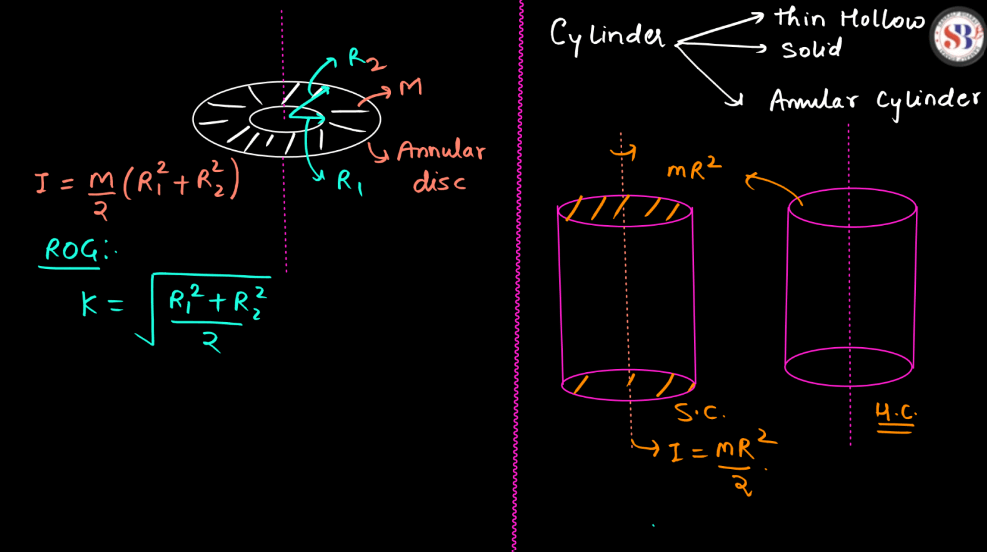
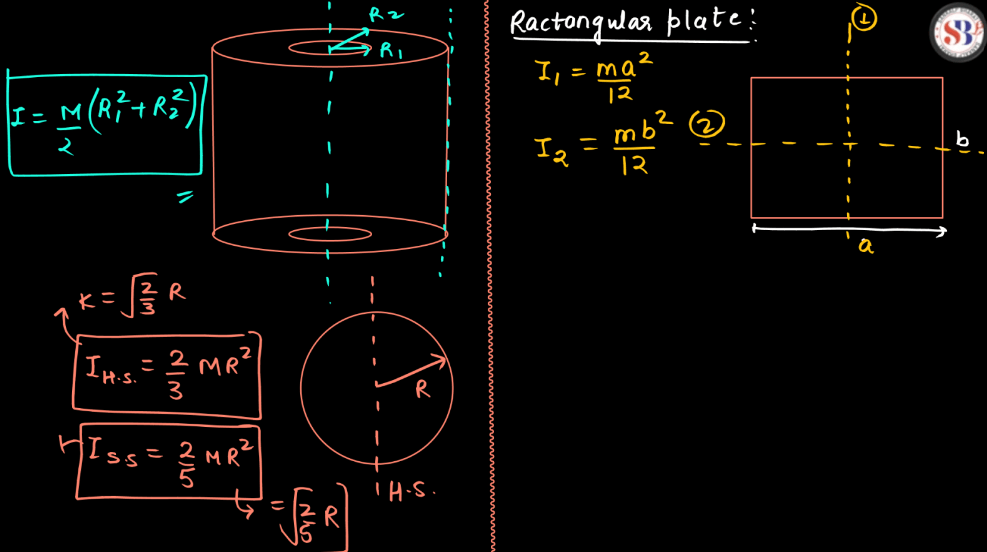
Moment of Inertia of a Distributed Mass Body

The moment of inertia of a distributed mass body is a measure of its resistance to rotational motion. Imagine spinning a bicycle wheel – the moment of inertia depends not only on the mass but also on how that mass is distributed relative to the axis of rotation. For a continuous object, like a rod or a disc, it involves integrating tiny mass elements at varying distances from the axis. The farther the mass is from the axis, the more it contributes to the moment of inertia. So, a body with mass spread out towards its edges will have a higher moment of inertia than a more centrally concentrated mass. This property plays a crucial role in understanding and predicting how objects rotate in response to applied torques.

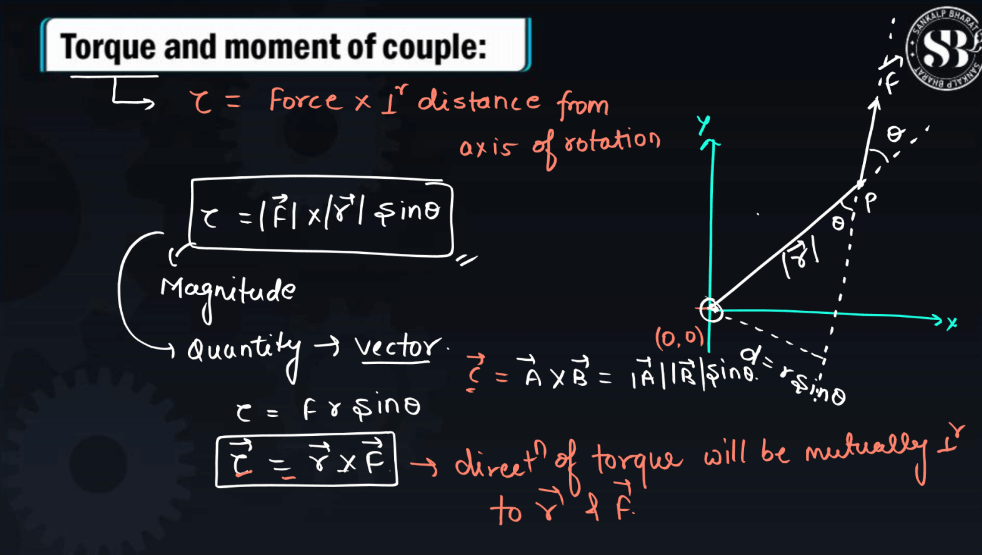
Define Torque

Torque is a measure of the turning forces applied to an object, causing it to rotate around an axis. Imagine trying to open a stubborn door – the forces you exert on the doorknob create torque. It depends on two factors: the force applied and the distance from the axis of rotation to the point where the force is applied. Think of it as a wrench turning a bolt – the longer the wrench or the greater the force applied, the more torque is generated. Mathematically, torque is calculated as the product of force and the perpendicular distance from the axis of rotation. In everyday terms, torque is what makes things spin or rotate, from the wheels of a car to the blades of a fan.

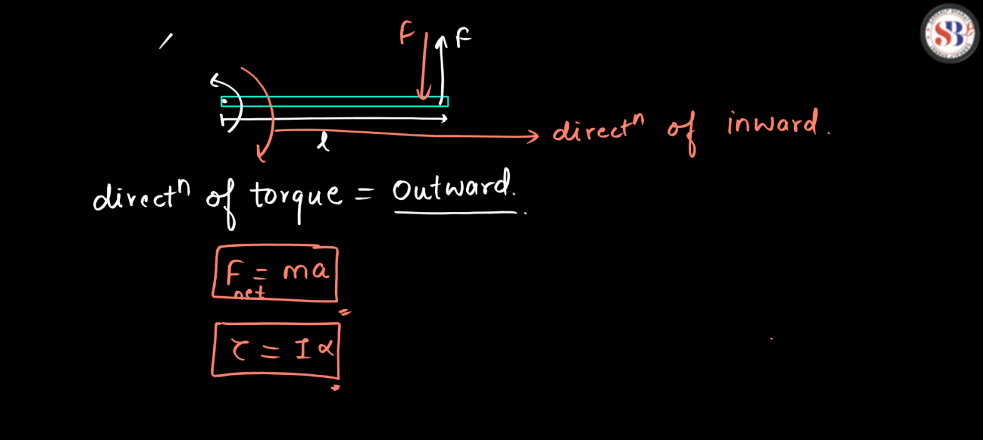
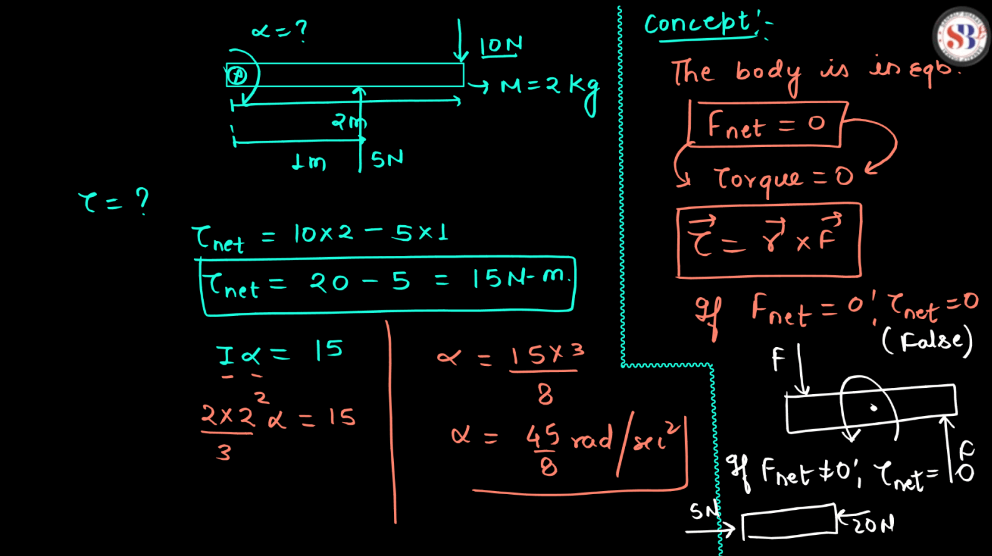
Want to learn more about Rotational Motion Dynamics, Watch the Video Below:

Sharing is caring!