What is the Center of Mass?
The center of mass is a point in an object or system where its mass can be considered to be concentrated. Imagine a seesaw – if you place a heavy object closer to the pivot, it balances a lighter object farther away. In simple terms, think of the center of mass as the “balancing point” of an object. It’s like locating the spot where an object would perfectly balance on your finger without tipping over. If an object is uniform and symmetrical, the center of mass aligns with its geometric center. However, irregular shapes or uneven mass distribution make it shift.
Picture a hanging mobile; each hanging piece has a different weight, but the mobile remains steady because the center of mass is carefully positioned. In everyday life, understanding the center of mass helps explain why certain objects are stable or why some activities, like tightrope walking, require careful consideration of weight distribution. Whether it’s a book on a shelf or a gymnast in mid-sir, the concept of center of mass plays a crucial role in explaining how objects behave and interact with forces.
Center of Gravity
The Center of Gravity (COG) is a point in an object where its entire mass can be considered to be concentrated. It’s the average position of all the individual mass particles, determining how the object behaves when subjected to gravity. In simple terms, if you could suspend an object from any point, the point where it would perfectly balance is its center of gravity. For symmetrical objects, the center of gravity aligns with the geometric center, but irregular shapes may have the center of gravity aligned with the geometric center, but irregular shapes may have the center of gravity in a different location. Understanding the Center of Gravity is crucial in designing stable structures and vehicles, as it influences their balance and stability. In summary, it’s the point where an object would perfectly balance, considering its mass distribution.
Importance of Center of Mass
The center of mass is crucial in Physics because it simplifies the description of motion for systems of particles. It behaves as if the entire mass of the system is concentrated at that point, making calculations more manageable. Additionally, understanding the center of mass is fundamental in studying stability, equilibrium, and predicting how objects move or interact in various physical scenarios.
- Simplifies Motion Analysis: The Center of mass allows for the simplification of complex systems by treating them as if all their mass were concentrated at a single point.
- Facilitates Calculations: Essential for making calculations related to motion, momentum, and collisions in physics, providing a more straightforward approach.
- Predicts Object Behavior: Understanding the center of mass helps predict how objects will move, rotate, or behave under the influence of forces, making it a key concept in mechanics.
- Stability and Equilibrium: Central in analyzing stability and equilibrium of objects or systems, aiding in designing structures or predicting the outcome of various physical situations.
- Uniform Gravitational Field: In a uniform gravitational field, the center of mass is the point where an object experiences gravitational forces as if all its mass were concentrated simplifying gravitational analyses.
What is a Rigid Body?
A rigid body is a simplified model in physics that assumes an object doesn’t deform or change shape when subjected to forces. Imagine a solid, unyielding object like a steel rod or a book. In this model, the distance between any two points on the object remains constant, allowing for straightforward analysis of motion and forces. It’s a useful approximation for studying motion, rotation, and equilibrium, especially when dealing with large, stiff objects. Keep in mind that in reality, deformations occur, but the rigid body concept simplifies calculations and aids in understanding fundamental principles of mechanics.
Formula of Center of Mass
The center of mass (CM) is a point in a system where the mass of the entire system can be considered to be concentrated. The formula for the center of mass involves finding the weighted average position of all the particles in the system. The center of mass (CM) formula for a system of particles is given by:
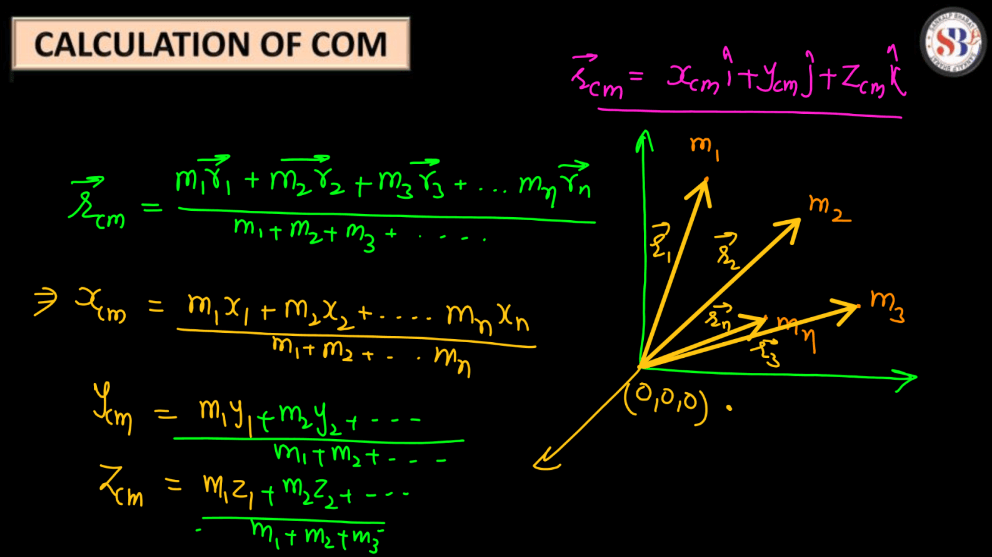
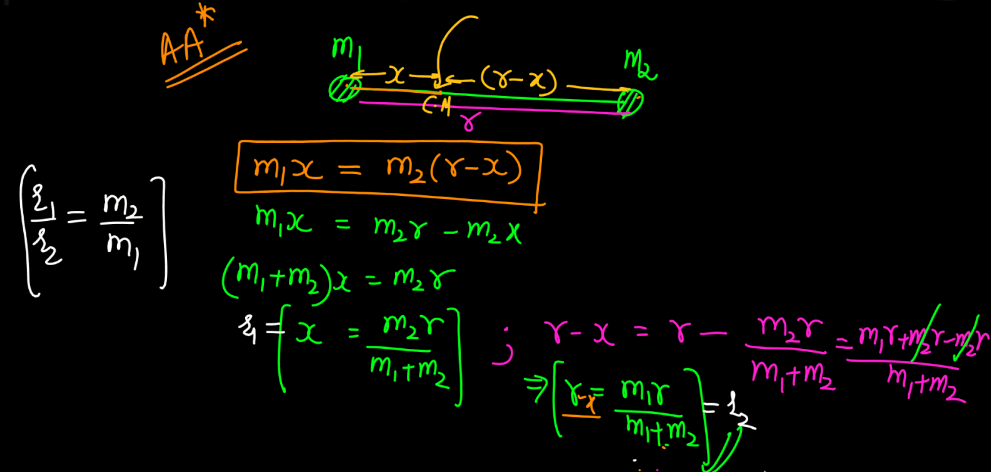
These equations calculate the coordinates of the center of mass in the x, y, and z directions, respectively. The numerators in each formula represent the sum of the products of individual masses and their respective coordinates, while the denominator is the total mass of the system. These equations provide a comprehensive way to determine the center of mass in three-dimensional space.
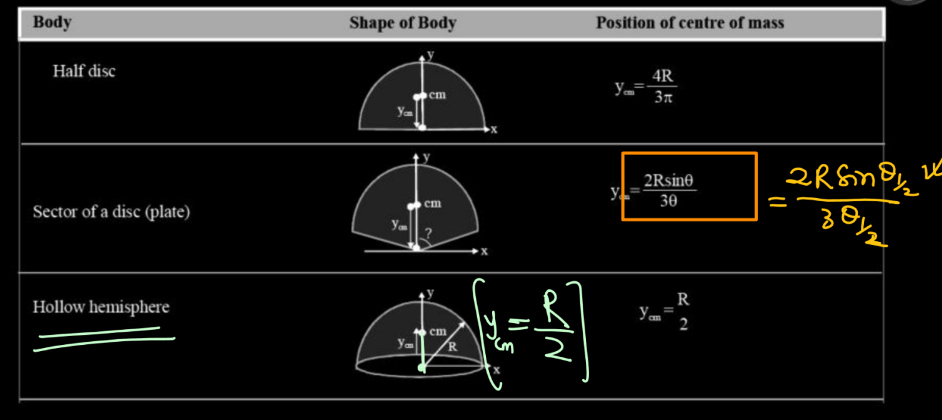
Position of Center of Mass in Different Shapes of Body
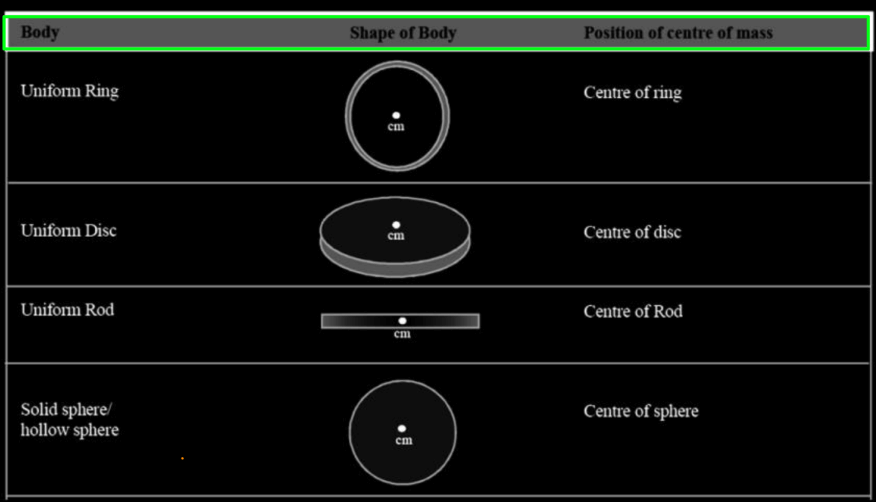
The center of mass is a point within an object where its mass is concentrated. In simple terms, for a symmetrical object like a sphere, the center of mass is at its geometric center. For a uniform rod, it’s at the midpoint. Irregular shapes might have their center of mass at a point where they would balance perfectly if placed on a narrow support.
MCQ related to the Center of Mass
Below we have discussed a few questions with their solutions related to the Center of Mass.






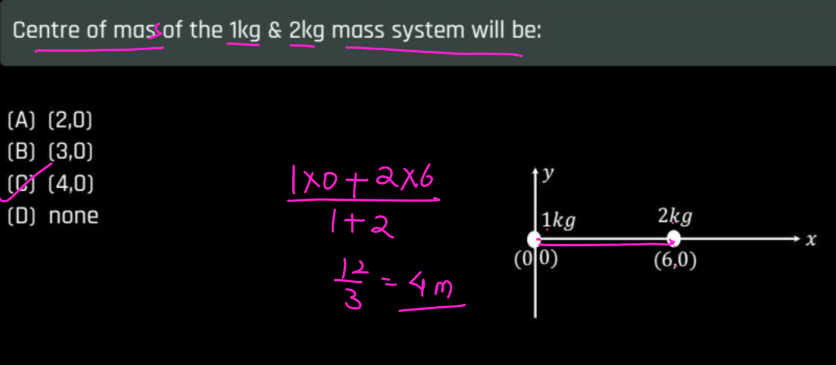


 Ohm's Law: Definition, Formula, Limitati...
Ohm's Law: Definition, Formula, Limitati...
 Newton's First Law of Motion: Definition...
Newton's First Law of Motion: Definition...
 Kepler's Laws of Planetary Motion: First...
Kepler's Laws of Planetary Motion: First...













