Order of Reaction
The order of a chemical reaction describes how the concentration of reactants affects the reaction rate. In simple terms, it’s like figuring out the recipe for a reaction. Imagine you’re baking cookies and the amount of flour and sugar you use influences how fast the cookies bake. Similarly, in chemistry, the order of reaction reveals how changes in the concentrations of reactant impact the speed of a reaction.
There are different orders: zero-order means the rate is independent of reactant concentration, first-order means the rate is directly proportional to one reactant’s concentration, and second-order indicates a dependence on the square of a reactant’s concentration. Knowing the order helps chemists predict how tweaking ingredients will affect the reaction rate, much like adjusting ingredients in a recipe alters baking time. It’s a way to understand and control chemical processes, making it a crucial concept in the realm of chemical kinetics.
Different Types of Order of Reaction
The order of a chemical reaction defines how the rate of reaction depends on the concentration of reactants. There are three main types of order of reactions namely: zero order reaction, First order reaction, and Second order reaction. These orders can be combined in more complex reactions. The overall order of a reaction is the sum of the individual orders. The order of reaction is determined experimentally by analyzing how the rate changes with varying reactant concentrations.
| Different Types of Order of Reactions | |
| Types | Description |
| Zero Order Reaction | The rate of the reaction is independent of the concentration of the reactants. The rate equation is typically expressed as Rate = k. |
| First Order Reaction | The rate is directly proportional to the concentration of one reactant. The rate equation is usually written as Rate = k[A] or Rate = k[B], where [A] or [B] is the concentration of the reactant. |
| Second Order Reaction | The rate is proportional to the square of the concentration of one reactant or to the product of the concentrations of two reactants. The rate equation can be expressed as Rate = k[A]^2 or Rate = k[A][B]. |
Zero Order Reaction
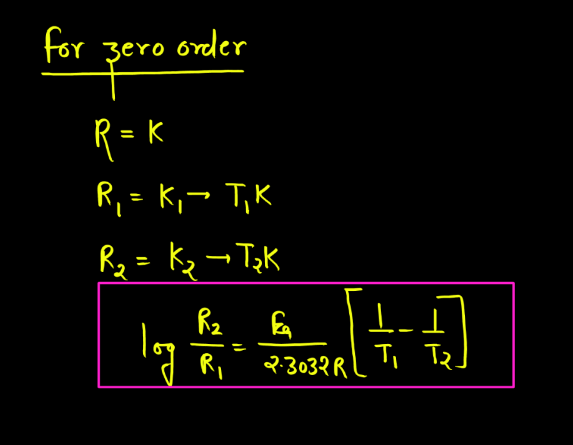
A zero-order reaction is a chemical reaction where the rate of reaction is independent of the concentration of the reactants. In simpler terms, the speed at which the reaction occurs doesn’t change, regardless of how much of the reactants are present. It’s like a fixed-speed assembly line; no matter how many workers (reactant molecules) you have, the products are made at a constant rate. Picture a conveyor belt moving at a steady pace – that’s analogous to a zero-order reaction. This reaction type is less common, and the concentration of the reactants remains constant over time, making it distinct from other reaction orders where concentration influences the reaction rate.
First Order Reaction
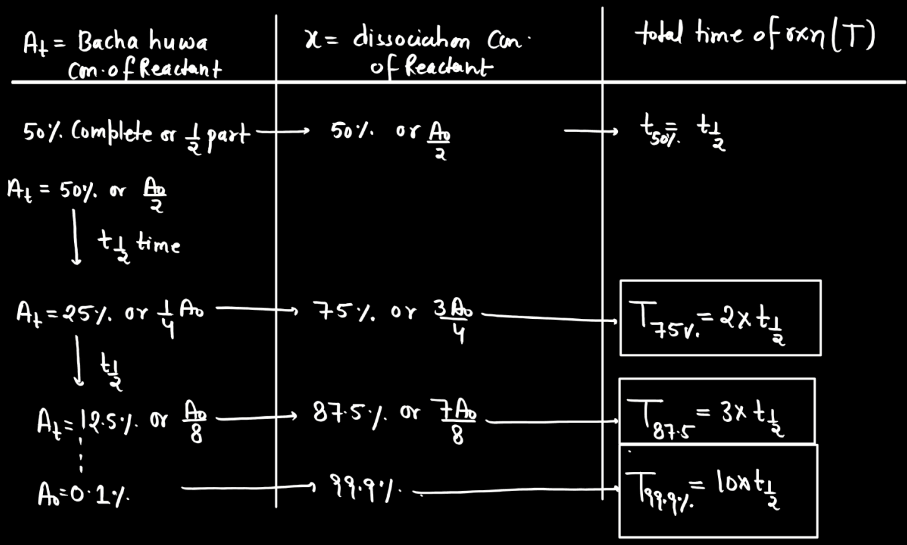
A first-order reaction describes a chemical process where the rate of reaction depends directly on the concentration of one reactant. In simpler terms, it means that as the concentration of this reactant decreases, the reaction slows down proportionally. The reaction rate is directly proportional to the concentration, implying that if you double the concentration, the rate will also double. Mathematically, the reaction rate (R) is expressed as R = k[A], where ‘k’ is the rate constant and ‘[A]’ is the concentration of the reactant. This type of reaction is common in scenarios like radioactive decay or certain chemical decompositions, providing a fundamental understanding of how reactions progress over time.

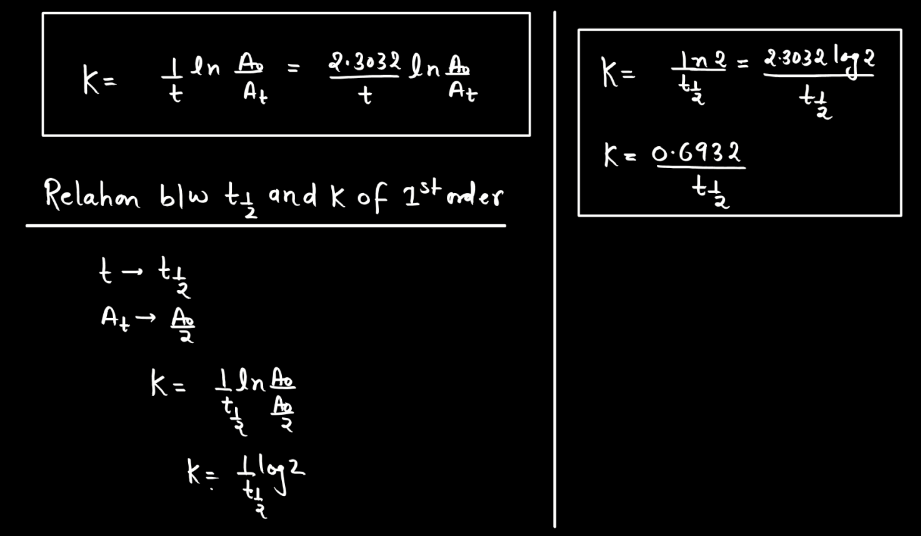


Second Order Reaction
A second-order reaction describes a chemical process where the rate of reaction is directly proportional to the square of the concentration of one reactant. In simpler terms, as the concentration of this reactant decreases, the rate of reaction diminishes even more rapidly compared to a first-order reaction. Mathematically, the reaction rate (R) is expressed as R = k[A]^2, where ‘k’ is the rate constant and ‘[A]’ is the concentration of the reactant. This type of reaction often involves two molecules colliding simultaneously for the reactions to occur. Second-order reactions are relevant in various contexts, such as chemical kinetics, where understanding how reactants interact and transform over time is crucial.

Characteristics of Order of Reaction
Understanding the order of reaction is crucial for predicting how changes in reactant concentrations will affect the reaction rate. The characteristics of an order of reaction include:
- Definition: The order of reaction defines how the rate of chemical reaction depends on the concentration of reactants.
- Mathematical Expression: It is expressed as a mathematical power, often denoted as “n”, a representation of the order with respect to a specific reactant. The overall order is the sum of individual orders.
- Units: The order of reaction is dimensionless and doesn’t have any specific units.
- Experimental Determination: Determined experimentally by analyzing how changes in reactant concentration affect the reaction rate.
- Reaction Rate Equation: The rate equation expresses the relationship between the rate of reaction and the concentrations of reactants raised to their respective order.
- Possible Values: The order can be zero, first, second, or even fractional or negative, depending on the reaction kinetics observed.
- Effect on Rate: The order influences how changes in reactant concentrations impact the rate of the reaction.
- Rate Constant: The rate constant (k) is associated with the overall order and represents the rate of reaction under specific conditions.
Different Methods to be Followed in Order to Determine the Reaction Order
There are several different methods that can be followed in order to determine the reaction order. Remember to perform experiments carefully, use appropriate instructions, and analyze the reaction order reliably.
- Initial Rate Method: Measure the initial rates of the reaction at different concentrations of reactants. The reaction order is determined by analyzing how changes in concentration affect the initial rate.
- Integrated Rate Laws: Integrate the rate equation with respect to concentration over time. Different reaction orders yield different integrated rate laws, helping to identify the correct order.
- Half-Life Method: Determine the half-life of the reaction at various concentrations. The relationship between half-life and concentration can reveal the reaction order.
- Graphical Methods: Plotting concentration vs. time or concentration vs. reaction rate can provide insights into the reaction order. For example, a straight line in a certain type of plot indicates a specific order.
- Initial Concentration vs. Initial Rate: Analyze how changes in the initial concentrations of reactants impact the initial rate of the reaction. This can help establish the reaction order.
Do watch the video, for a detailed study


 Modes of Heat Transfer with Examples
Modes of Heat Transfer with Examples
 Evaporation - Definition, Step-Wise Proc...
Evaporation - Definition, Step-Wise Proc...
 What is Sedimentation, Decantation and F...
What is Sedimentation, Decantation and F...













