Zero Order Reaction – Definition, Graph, Equation, Derivation

Define Zero Order Reaction

A Zero Order reaction is a chemical process where the rate of reaction is independent where the rate of reaction is independent of the concentration of the reactants. In simpler terms, it means that no matter how much you increase or decrease the amount of reactants, the speed at which the reaction occurs remains constant. Picture it like a car moving at a fixed speed – whether there are a lot of cars on the road (high concentration) or just a few (low concentration), the car maintains the same speed.

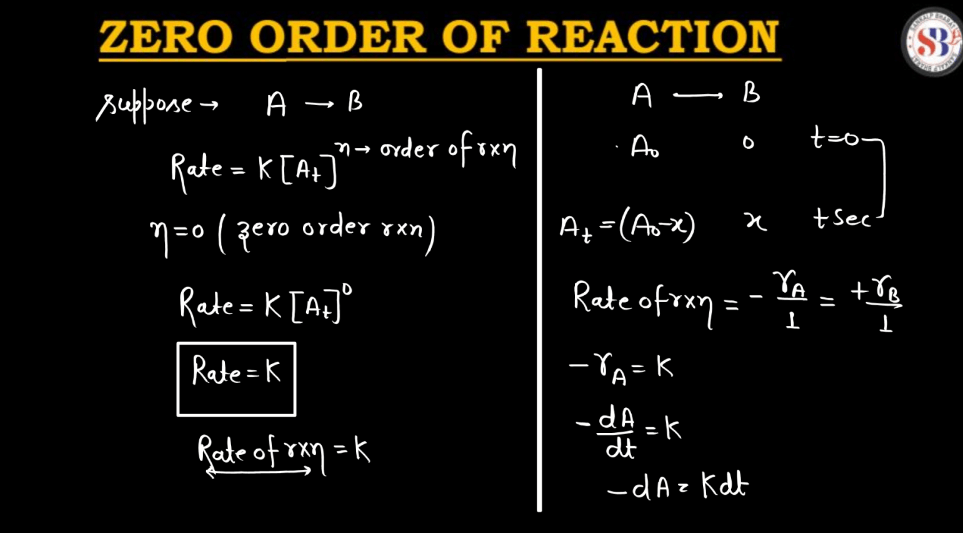
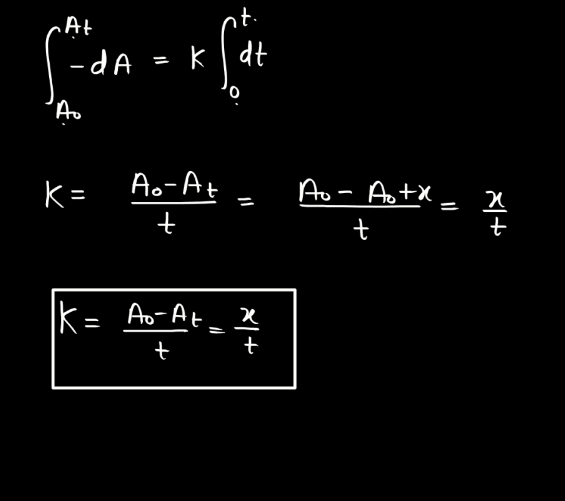
For a Zero Order reaction, the rate of reaction is determined by other factors, such as temperature or catalyst presence, rather than the amount of reactants. This makes Zero Order reactions unique compared to first-order or second-order reactions, where the rate is directly proportional to the concentration of the reactants. Understanding these reaction orders is crucial for predicting and controlling chemical reactions in various industrial and scientific applications.

Characteristics of Zero Order Reaction

Below we have discussed a few characteristics of Zero Order creation. These characteristics make Zero Order reactions unique and are often encountered in situations where the reaction rate is limited by factors other than reactant concentrations.

1. Constant Reation: In a Zero Order reaction, the rate of the reaction remains constant over time. The rate is independent of the concentration of the reactant(s).
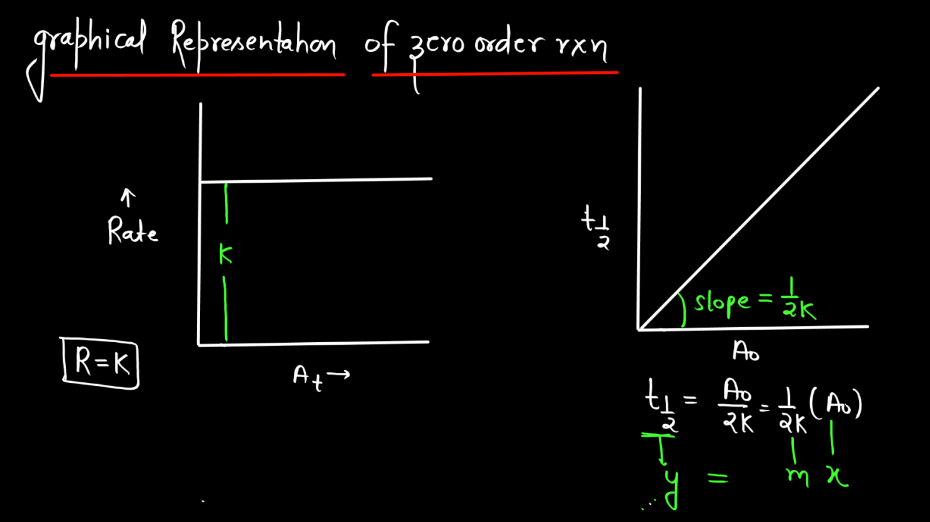
2. Graphical Representation: The concentration of the reactant versus time graph yields a straight line with a negative slope in a Zero Order reaction, making it visually distinct from other reaction orders.
3. Half-Life Independence: Unlike first-order reactions, Zero Order reactions do not have a constant half-life. The time taken for the concentration to reduce by half is not fixed but depends on the initial concentration.
4. Reaction Rate Expression: The rate expression for a Zero Order reaction is expressed as Rate = k, where k is the rate constant.
5. Concentration Depletion Effect: As the reaction progresses, the reactant concentration decreases linearly with time in a Zero Order reaction, leading to a steady depletion of the reactant.

Half-Life of Zero Order Reaction

In a Zero Order reaction, the rate of the reaction is independent of the concentration of the reactant. The half-life (t_1/2) of a Zero Order reaction is the time required for half of the initial concentration of the reactant to be consumed. This means that, unlike first-order reactions where the rate is directly proportional to the concentration, in a Zero Order reaction, the half-life changes as the creation progresses. The formula for the half-life (t_1/2) of Zero Order reaction is given by:

t_1/2 = [A]₀/2k

Where:

• [A]₀ is the initial concentration of the reactant,
• whereas k is the rate constant of the reaction.

What’s most interesting in Zero Order reactions is that as the reaction progresses, the concentration of reactant decreases. Consequently, the half-life increases over time. In other words, the time it takes to consume half of the remaining reactant becomes longer as the reaction proceeds. This is in contrast to first-order reactions where the half-life remains constant regardless of the initial concentration. In Zero Order reactions, the rate of reactions is intricately tied to the initial concentration, providing a different perspective on reaction kinetics compared to other orders.

Differential and Integral Form of Zero Order Reaction

A Zero Order reaction is a chemical reaction where the rate of reaction is independent of the concentration of the reactant. This means that, unlike first-order or second-order reactions, doubling or having the concentration of the reactant does not affect the rate of reaction.

Differential Reaction:

The differential form of a Zero Order reaction is expressed as:

Let’s denote the concentration of the reactant as [A]. The rate law for a Zero Order reaction is expressed as:

– d[A]/dt = k

Here,

• – d[A]/dt represents the rate at which the concentration of reactant changes with respect to time.
• And k is the rate constant, which is a constant value of a given reaction at a specific temperature.

This equation essentially states that the rate of reaction in the concentration of A is directly proportional to the rate constant k.

Integral Form

To obtain the integral form, we need to intricate the differential equation.

Now, let us integrate the above differentiation equation. Assume the initial concentration of the reactant [A]₀ at t = 0, the integral form is:

[A]_t = [A]₀ – kt

In this equation:

• [A]_t is the concentration of A at time t.
• [A]₀ is the initial concentration of A.
• k is the rate constant.

This integral form shows that the concentration of A decreases linearly with time in a Zero Order reaction. The larger the rate constant K, the faster the reaction proceeds.

Summary:

In a nutshell, for a Zero Order reaction:

1. The rate of reaction is constant and independent of the reactant concentration.
2. The differential form relates the rate of change of concentration to the rate constant.
3. The integral form shows the concentration decreases linearly with time.

Graph of Zero Order Reaction

In a zero order reaction, the rate of the reaction is independent of the concentration of the reactant. This means that the reaction proceeds at a constant rate regardless of how much reactant is present. The graph of Zero Order reaction typically shows the concentration of the reactant over time. It appears as a straight line with a negative slope, indicating a constant rate of reaction. The equation for the concentration of the reactant ([A]) as a function of time (t) in a Zero Order reaction is:

[A] = –kt + [A]₀

Where:

• [A] is the concentration of the reactant at time t,
• k is the rate constant,
• t is the time, and
• [A]₀ is the initial concentration of the reactant.

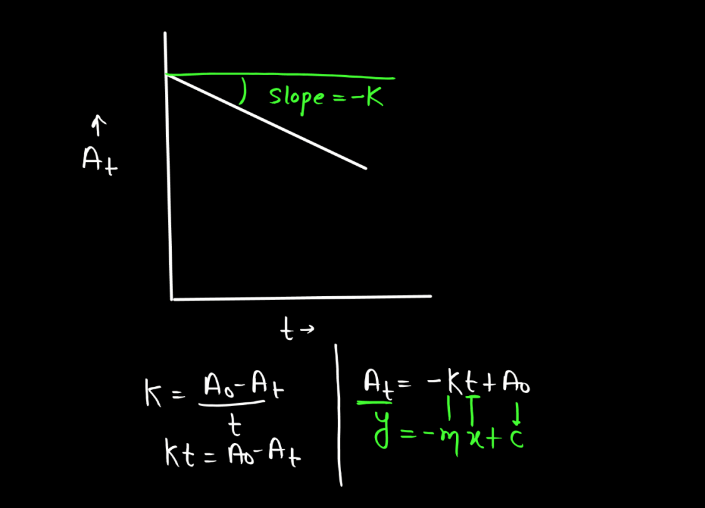
In this graph, the slope is equal to –k, the rate constant and the intercept on the y-axis is the initial concentration [A]₀. The linear nature of the graph distinguishes Zero Order reactions from first and second-order reactions.

Sharing is caring!